Papers

Random access codes have provided many examples of quantum advantage in communication, but concern only one kind of information retrieval task. We introduce a related task—the Torpedo Game—and show that it admits greater quantum advantage than the comparable random access code. Perfect quantum strategies involving prepare-and-measure protocols with experimentally accessible three-level systems emerge via analysis in terms of the discrete Wigner function. The example is leveraged to an operational advantage in a pacifist version of the strategy game Battleship. We pinpoint a characteristic of quantum systems that enables quantum advantage in any bounded-memory information retrieval task. While preparation contextuality has previously been linked to advantages in random access coding we focus here on a different characteristic called sequential contextuality. It is shown not only to be necessary and sufficient for quantum advantage, but also to quantify the degree of advantage. Our perfect qutrit strategy for the Torpedo Game entails the strongest type of inconsistency with noncontextual hidden variables, revealing logical paradoxes with respect to those assumptions.

We establish lower-bounds on the number of resource states, also known as magic states, needed to perform various quantum computing tasks, treating stabilizer operations as free. Our bounds apply to adaptive computations using measurements and an arbitrary number of stabilizer ancillas. We consider (1) resource state conversion, (2) single-qubit unitary synthesis, and (3) computational tasks. To prove our resource conversion bounds we introduce two new monotones, the stabilizer nullity and the dyadic monotone, and make use of the already-known stabilizer extent. We consider conversions that borrow resource states, known as catalyst states, and return them at the end of the algorithm. We show that catalysis is necessary for many conversions and introduce new catalytic conversions, some of which are close to optimal. By finding a canonical form for post-selected stabilizer computations, we show that approximating a single-qubit unitary to within diamond-norm precision ε requires at least 1/7⋅log2(1/ε)−4/3 T-states on average. This is the first lower bound that applies to synthesis protocols using fall-back, mixing techniques, and where the number of ancillas used can depend on ε. Up to multiplicative factors, we optimally lower bound the number of T or CCZ states needed to implement the ubiquitous modular adder and multiply-controlled-Z operations. When the probability of Pauli measurement outcomes is 1/2, some of our bounds become tight to within a small additive constant.

Recent work has explored using the stabilizer formalism to classically simulate quantum circuits containing a few non-Clifford gates. The computational cost of such methods is directly related to the notion of stabilizer rank, which for a pure state ψ is defined to be the smallest integer χ such that ψ is a superposition of χ stabilizer states. Here we develop a comprehensive mathematical theory of the stabilizer rank and the related approximate stabilizer rank. We also present a suite of classical simulation algorithms with broader applicability and significantly improved performance over the previous state-of-the-art. A new feature is the capability to simulate circuits composed of Clifford gates and arbitrary diagonal gates, extending the reach of a previous algorithm specialized to the Clifford+T gate set. We implemented the new simulation methods and used them to simulate quantum algorithms with 40-50 qubits and over 60 non-Clifford gates, without resorting to high-performance computers. We report a simulation of the Quantum Approximate Optimization Algorithm in which we process superpositions of χ∼10^6 stabilizer states and sample from the full n-bit output distribution, improving on previous simulations which used ∼10^3 stabilizer states and sampled only from single-qubit marginals. We also simulated instances of the Hidden Shift algorithm with circuits including up to 64 T gates or 16 CCZ gates; these simulations showcase the performance gains available by optimizing the decomposition of a circuit's non-Clifford components.

Magic states are eigenstates of non-Pauli operators. One way of suppressing errors present in magic states is to perform parity measurements in their non-Pauli eigenbasis and postselect on even parity. Here we develop new protocols based on non-Pauli parity checking, where the measurements are implemented with the aid of pre-distilled multiqubit resource states. This leads to a two step process: pre-distillation of multiqubit resource states, followed by implementation of the parity check. These protocols can prepare single-qubit magic states that enable direct injection of single-qubit axial rotations without subsequent gate-synthesis and its associated overhead. We show our protocols are more efficient than all previous comparable protocols with quadratic error reduction, including the protocols of Bravyi and Haah.

Motivated by their necessity for most fault-tolerant quantum computation schemes, we formulate a resource theory for magic states. First, we show that robustness of magic is a well-behaved magic monotone that operationally quantifies the classical simulation overhead for a Gottesman-Knill-type scheme using ancillary magic states. Our framework subsequently finds immediate application in the task of synthesizing non-Clifford gates using magic states. When magic states are interspersed with Clifford gates, Pauli measurements, and stabilizer ancillas—the most general synthesis scenario—then the class of synthesizable unitaries is hard to characterize. Our techniques can place nontrivial lower bounds on the number of magic states required for implementing a given target unitary. Guided by these results, we have found new and optimal examples of such synthesis.

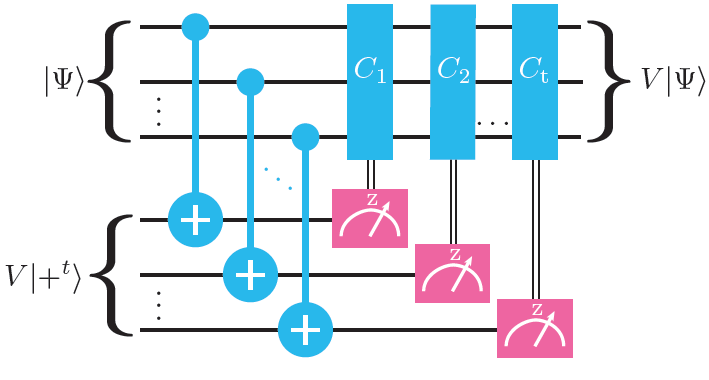
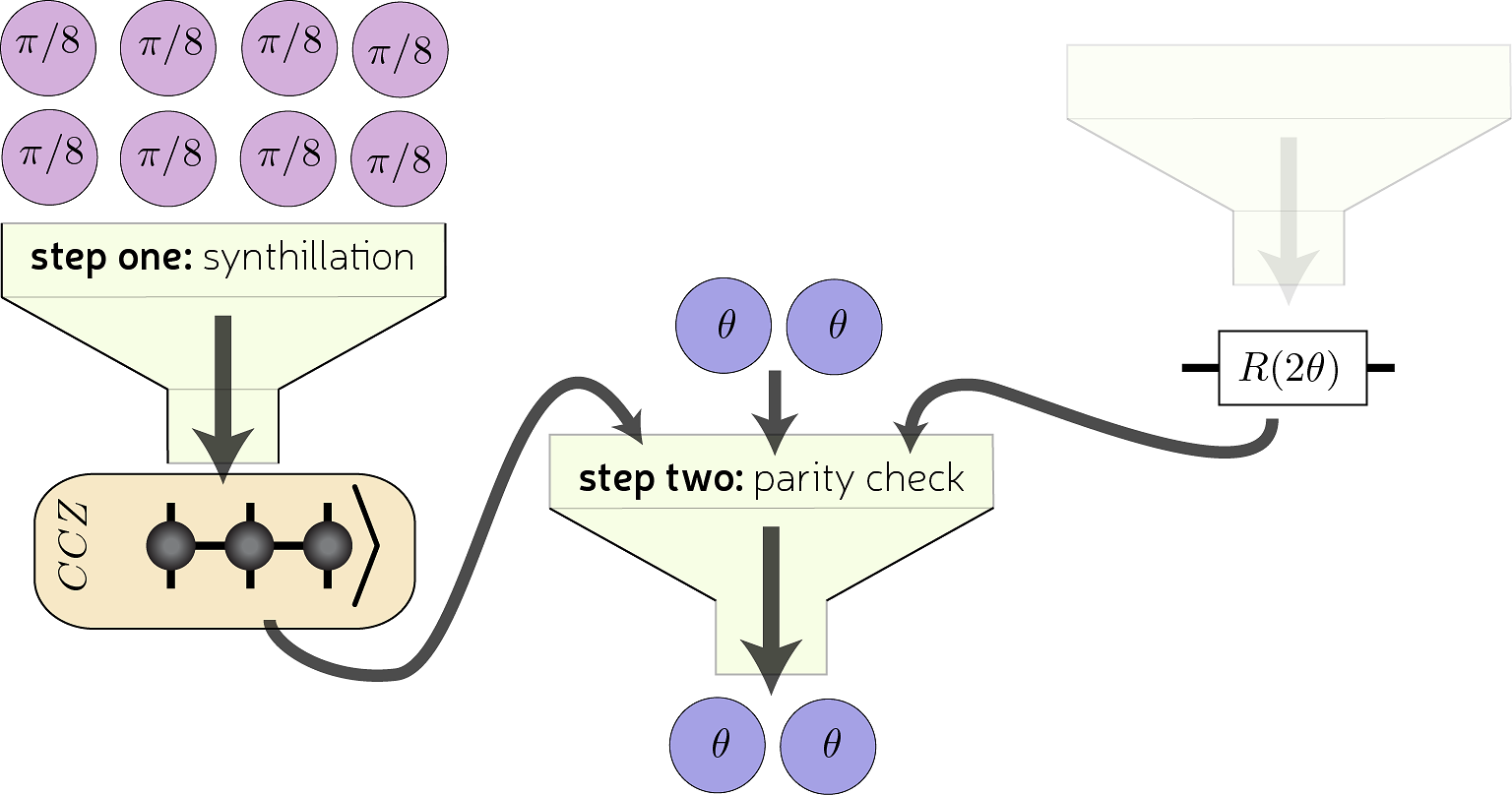
The standard approach to fault-tolerant quantum computation is to store information in a quantum error correction code, such as the surface code, and process information using a strategy that can be summarized as distill then synthesize. In the distill step, one performs several rounds of distillation to create high-fidelity logical qubits in a magic state. Each such magic state provides one good T gate. In the synthesize step, one seeks the optimal decomposition of an algorithm into a sequence of many T gates interleaved with Clifford gates. This gate-synthesis problem is well understood for multiqubit gates that do not use any Hadamards. We present an in-depth analysis of a unified framework that realizes one round of distillation and multiqubit gate synthesis in a single step. We call these synthillation protocols, and show they lead to a large reduction in resource overheads. This is because synthillation can implement a general class of circuits using the same number of T states as gate synthesis, yet with the benefit of quadratic error suppression. This general class includes all circuits primarily dominated by control-control-Z gates, such as adders and modular exponentiation routines used in Shor's algorithm. Therefore, synthillation removes the need for a costly round of magic state distillation. We also present several additional results on the multiqubit gate-synthesis problem. We provide an efficient algorithm for synthesizing unitaries with the same worst-case resource scaling as optimal solutions. For the special case of synthesizing controlled unitaries, our techniques are not just efficient but exactly optimal. We observe that the gate-synthesis cost, measured by T count, is often strictly subadditive. Numerous explicit applications of our techniques are also presented.

The leading paradigm for performing a computation on quantum memories can be encapsulated as distill-then-synthesize. Initially, one performs several rounds of distillation to create high-fidelity magic states that provide one good T gate, an essential quantum logic gate. Subsequently, gate synthesis intersperses many T gates with Clifford gates to realize a desired circuit. We introduce a unified framework that implements one round of distillation and multiquibit gate synthesis in a single step. Typically, our method uses the same number of T gates as conventional synthesis but with the added benefit of quadratic error suppression. Because of this, one less round of magic state distillation needs to be performed, leading to significant resource savings.

Magic state distillation is a critical component in leading proposals for fault-tolerant quantum computation. Relatively little is known, however, about how to construct a magic state distillation routine or, more specifically, which stabilizer codes are suitable for the task. While transversality of a non-Clifford gate within a code often leads to efficient distillation routines, it appears to not be a necessary condition. Here we have examined a number of small stabilizer codes and highlight a handful of which displaying interesting, albeit inefficient, distillation behaviour. Many of these distill noisy states right up to the boundary of the known undististillable region, while some distill toward non-stabilizer states that have not previously been considered.

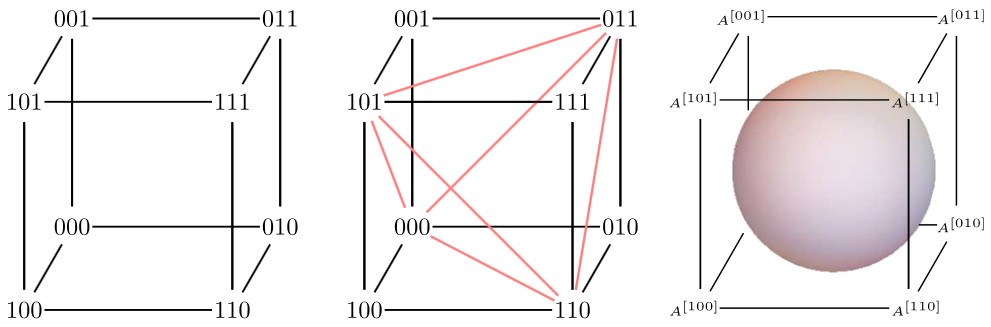
We present a construction of Hermitian operators and quantum states labelled by strings from a finite field. The distance between these operators or states is then simply related (typically, proportional) to the Hamming distance between their corresponding strings. This allows a straightforward application of classical coding theory to find arrangements of operators or states with a given distance distribution. Using the simplex or extended Reed–Solomon code in our construction recovers the discrete Wigner function, which has important applications in quantum information theory.

Magic state distillation is a crucial component in the leading approaches to implementing universal fault-tolerant quantum computation, with existing protocols for both qubit and higher dimensional systems. Early work focused on determining the region of distillable states for qubit protocols; yet comparatively little is known about which states can be distilled and with what distillable region for d>2. Here we focus on d=3 and present new four-qutrit distillation schemes that improve upon the known distillable region, and achieve distillation tight to the boundary of undistillable states for some classes of state. As a consequence of recent results, this implies that there is a family of quantum states that enable universality if and only if they exhibit contextuality with respect to stabilizer measurements. We also identify a new routine whose fixed point is a magic state with maximal sum negativity; i.e., it is maximally nonstablizer in a specific sense.

We prove that magic states from the Clifford hierarchy give optimal solutions for tasks involving nonlocality and entropic uncertainty with respect to Pauli measurements. For both the nonlocality and uncertainty tasks, stabilizer states are the worst possible pure states, so our solutions have an operational interpretation as being highly nonstabilizer. The optimal strategy for a qudit version of the Clauser-Horne-Shimony-Holt game in prime dimensions is achieved by measuring maximally entangled states that are isomorphic to single-qudit magic states. These magic states have an appealingly simple form, and our proof shows that they are “balanced” with respect to all but one of the mutually unbiased stabilizer bases. Of all equatorial qudit states, magic states minimize the average entropic uncertainties for collision entropy and also, for small prime dimensions, min-entropy, a fact that may have implications for cryptography.

We investigate the action of the first three levels of the Clifford hierarchy on sets of mutually unbiased bases comprising the Ivanovic mutually unbiased base (MUB) and the Alltop MUBs. Vectors in the Alltop MUBs exhibit additional symmetries when the dimension is a prime number equal to 1 modulo 3 and thus the set of all Alltop vectors splits into three Clifford orbits. These vectors form configurations with so-called Zauner subspaces, eigenspaces of order 3 elements of the Clifford group highly relevant to the SIC problem. We identify Alltop vectors as the magic states that appear in the context of fault-tolerant universal quantum computing, wherein the appearance of distinct Clifford orbits implies a surprising inequivalence between some magic states.

Quantum computers promise dramatic advantages over their classical counterparts, but the source of the power in quantum computing has remained elusive. Here we prove a remarkable equivalence between the onset of contextuality and the possibility of universal quantum computation via ‘magic state’ distillation, which is the leading model for experimentally realizing a fault-tolerant quantum computer. This is a conceptually satisfying link, because contextuality, which precludes a simple ‘hidden variable’ model of quantum mechanics, provides one of the fundamental characterizations of uniquely quantum phenomena. Furthermore, this connection suggests a unifying paradigm for the resources of quantum information: the non-locality of quantum theory is a particular kind of contextuality, and non-locality is already known to be a critical resource for achieving advantages with quantum communication. In addition to clarifying these fundamental issues, this work advances the resource framework for quantum computation, which has a number of practical applications, such as characterizing the efficiency and trade-offs between distinct theoretical and experimental schemes for achieving robust quantum computation, and putting bounds on the overhead cost for the classical simulation of quantum algorithms.

The Pauli groups are ubiquitous in quantum information theory because of their usefulness in describing quantum states and operations and their readily understood symmetry properties. In addition, the most well-understood quantum error correcting codes—stabilizer codes—are built using Pauli operators. The eigenstates of these operators—stabilizer states—display a structure (e.g., mutual orthogonality relationships) that has made them useful in examples of multi-qubit non-locality and contextuality. Here, we apply the graph-theoretical contextuality formalism of Cabello, Severini and Winter to sets of stabilizer states, with particular attention to the effect of generalizing two-level qubit systems to odd prime d-level qudit systems. While state-independent contextuality using two-qubit states does not generalize to qudits, we show explicitly how state-dependent contextuality associated with a Bell inequality does generalize. Along the way we note various structural properties of stabilizer states, with respect to their orthogonality relationships, which may be of independent interest.

When visualized as an operation on the Bloch sphere, the qubit π/8 gate corresponds to 1/8 of a complete rotation about the vertical axis. This simple gate often plays an important role in quantum information theory, typically in situations for which Pauli and Clifford gates are insufficient. Most notably, if it supplements the set of Clifford gates, then universal quantum computation can be achieved. The π/8 gate is the simplest example of an operation from the third level of the Clifford hierarchy (i.e., it maps Pauli operations to Clifford operations under conjugation). Here we derive explicit expressions for all qudit (d-level, where d is prime) versions of this gate and analyze the resulting group structure that is generated by these diagonal gates. This group structure differs depending on whether the dimensionality of the qudit is two, three, or greater than three. We then discuss the geometrical relationship of these gates (and associated states) with respect to Clifford gates and stabilizer states. We present evidence that these gates are maximally robust to depolarizing and phase-damping noise, in complete analogy with the qubit case. Motivated by this and other similarities, we conjecture that these gates could be useful for the task of qudit magic-state distillation and, by extension, fault-tolerant quantum computing. Very recently, independent work by Campbell et al. confirmed the correctness of this intuition, and we build upon their work to characterize noise regimes for which noisy implementations of these gates can (or provably cannot) supplement Clifford gates to enable universal quantum computation.

An obstacle affecting any proposal for a topological quantum computer based on Ising anyons is that quasiparticle braiding can only implement a finite (nonuniversal) set of quantum operations. The computational power of this restricted set of operations (often called stabilizer operations) has been studied in quantum information theory, and it is known that no quantum-computational advantage can be obtained without the help of an additional nonstabilizer operation. Similarly, a bipartite two-qubit system based on Ising anyons can not exhibit nonlocality (in the sense of violating a Bell inequality) when only topologically protected stabilizer operations are performed. To produce correlations that can not be described by a local hidden variable model again requires the use of a nonstabilizer operation. Using geometric techniques, we relate the sets of operations that enable universal quantum computing (UQC) with those that enable violation of a Bell inequality. Motivated by the fact that nonstabilizer operations are expected to be highly imperfect, our aim is to provide a benchmark for identifying UQC-enabling operations that is both experimentally practical and conceptually simple. We show that any (noisy) single-qubit nonstabilizer operation that, together with perfect stabilizer operations, enables violation of the simplest two-qubit Bell inequality, can also be used to enable UQC. This benchmarking requires finding the expectation values of two distinct Pauli measurements on each qubit of a bipartite system.

We examine the existence and structure of particular sets of mutually unbiased bases (MUBs) in bipartite qudit systems. In contrast to well-known power-of-prime MUB constructions, we restrict ourselves to using maximally entangled stabilizer states as MUB vectors. Consequently, these bipartite entangled stabilizer MUBs (BES MUBs) provide no local information, but are sufficient and minimal for decomposing a wide variety of interesting operators including (mixtures of) Jamiołkowski states, entanglement witnesses, and more. The problem of finding such BES MUBs can be mapped, in a natural way, to that of finding maximum cliques in a family of Cayley graphs. Some relationships with known power-of-prime MUB constructions are discussed, and observables for BES MUBs are given explicitly in terms of Pauli operators.

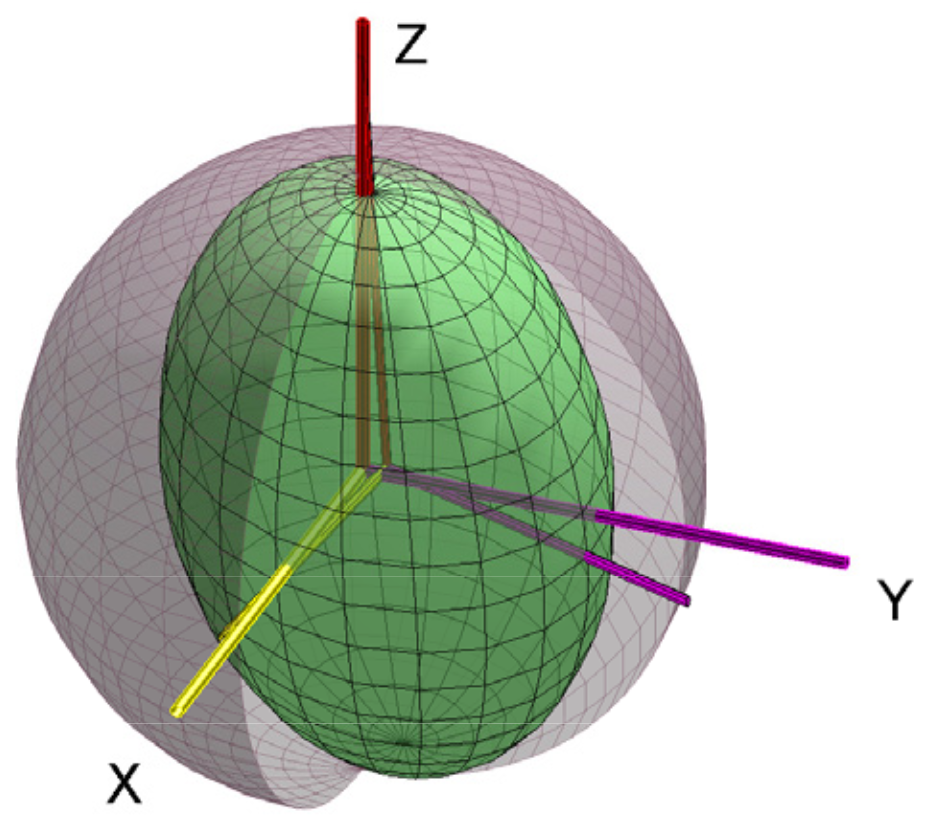
For a quantum computer acting on d-dimensional systems, we analyze the computational power of circuits wherein stabilizer operations are perfect, and we allow access to imperfect nonstabilizer states or operations. If the noise rate affecting the nonstabilizer resource is sufficiently high, then these states and operations can become simulable in the sense of the Gottesman-Knill theorem, reducing the overall power of the circuit to no better than classical. In this paper we find the depolarizing noise rate at which this happens and consequently the most robust nonstabilizer states and non-Clifford gates. In doing so, we make use of the discrete Wigner function and derive facets of the so-called qudit Clifford polytope, i.e., the inequalities defining the convex hull of all qudit Clifford gates. Our results for robust states are provably optimal. For robust gates we find a critical noise rate that, as dimension increases, rapidly approaches the the theoretical optimum of 100%. Some connections with the question of qudit magic state distillation are discussed.

We study how much noise can be tolerated by a universal gate set before it loses its quantum-computational power. Specifically we look at circuits with perfect stabilizer operations in addition to imperfect nonstabilizer gates. We prove that for all unitary single-qubit gates there exists a tight depolarizing noise threshold that determines whether the gate enables universal quantum computation or if the gate can be simulated by a mixture of Clifford gates. This exact threshold is determined by the Clifford polytope spanned by the 24 single-qubit Clifford gates. The result is in contrast to the situation wherein nonstabilizer qubit states are used; the thresholds in that case are not currently known to be tight.

We present an example of quantum process tomography (QPT) performed on a single solid-state qubit. The qubit used is two energy levels of the triplet state in the nitrogen vacancy defect in diamond. QPT is applied to a qubit which has been allowed to decohere for three different time periods. In each case, the process is found in terms of the χ matrix representation and the affine map representation. The discrepancy between experimentally estimated process and the closest physically valid process is noted. The results of QPT performed after three different decoherence times are used to find the error generators, or Lindblad operators, for the system, using the technique introduced by Boulant et al (2003 Phys. Rev. A 67 042322).