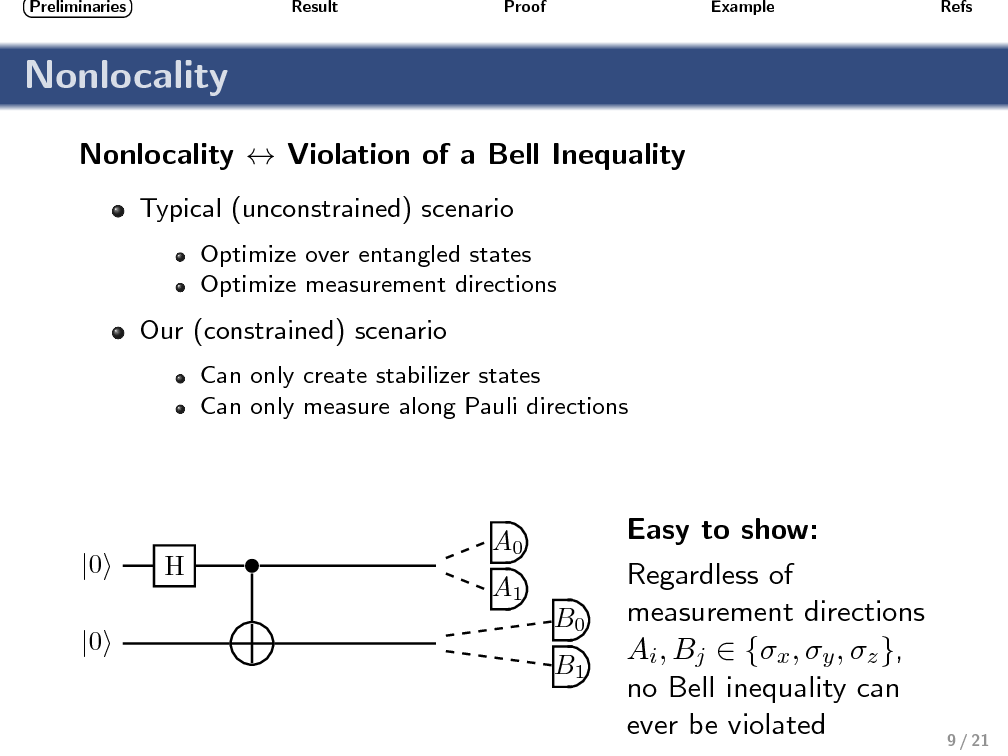
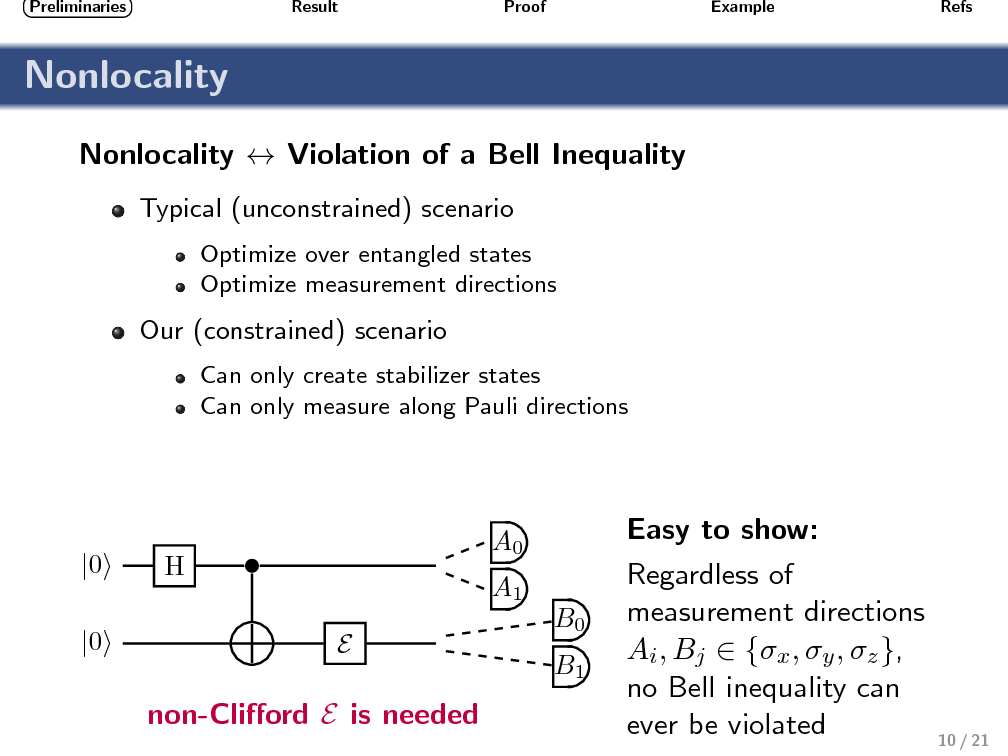
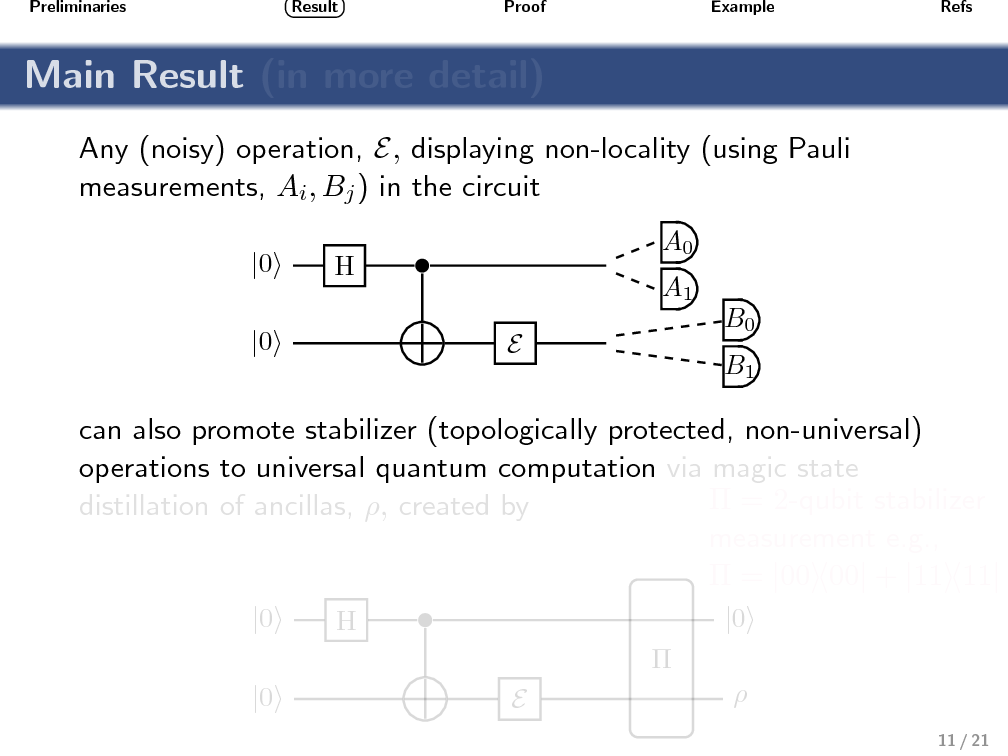
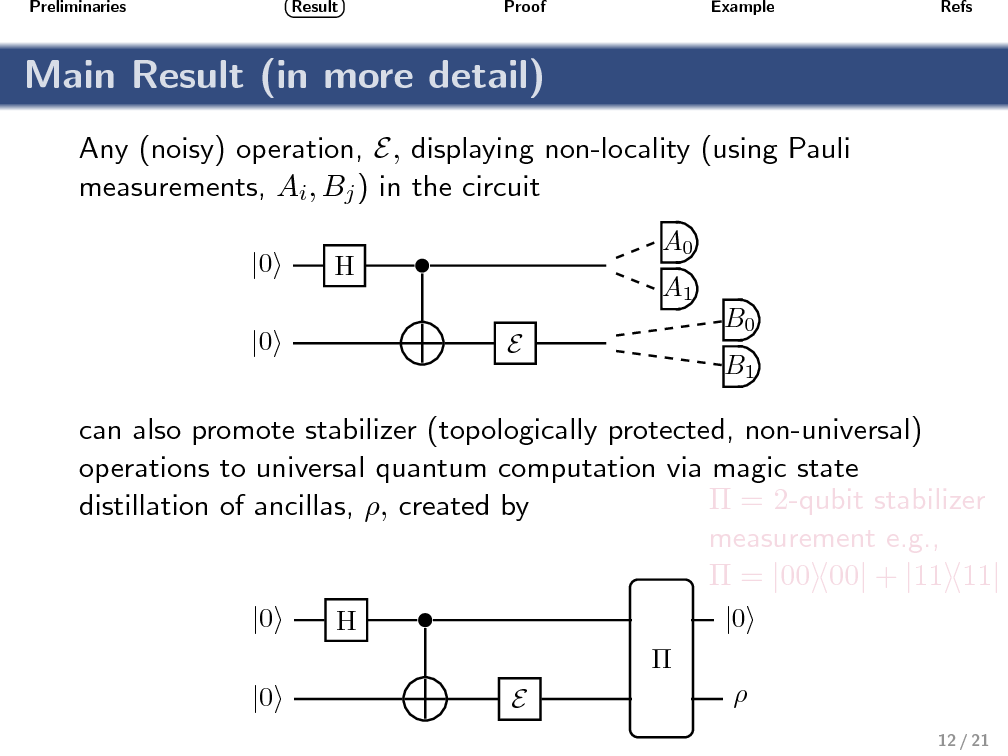
Nonlocality as a Benchmark for Universal Quantum Computation
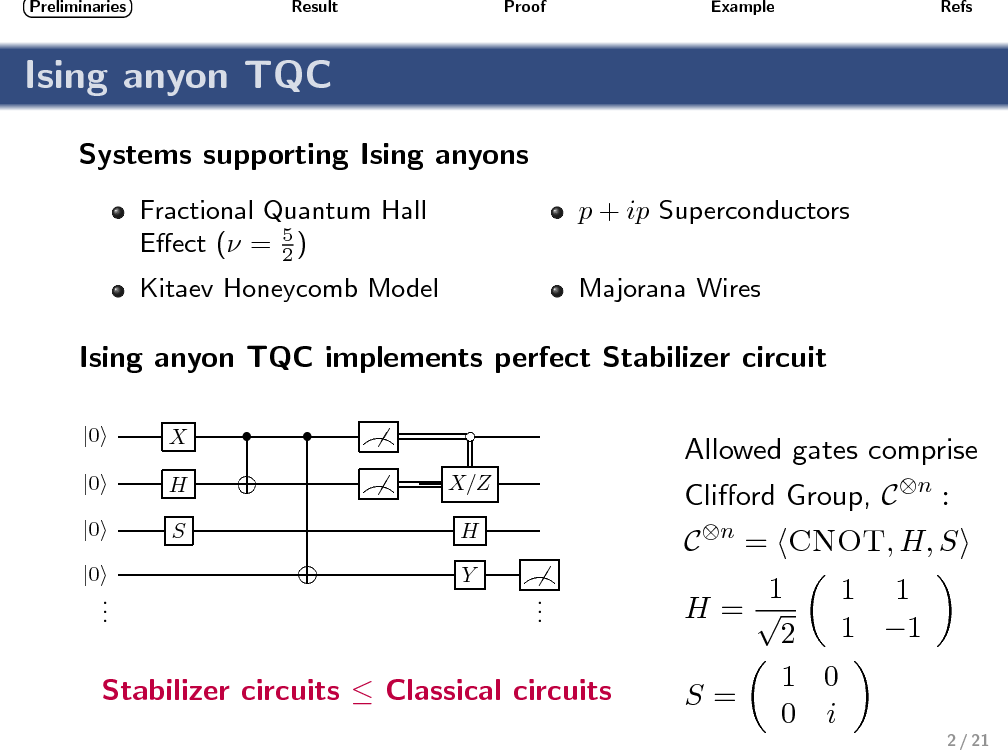
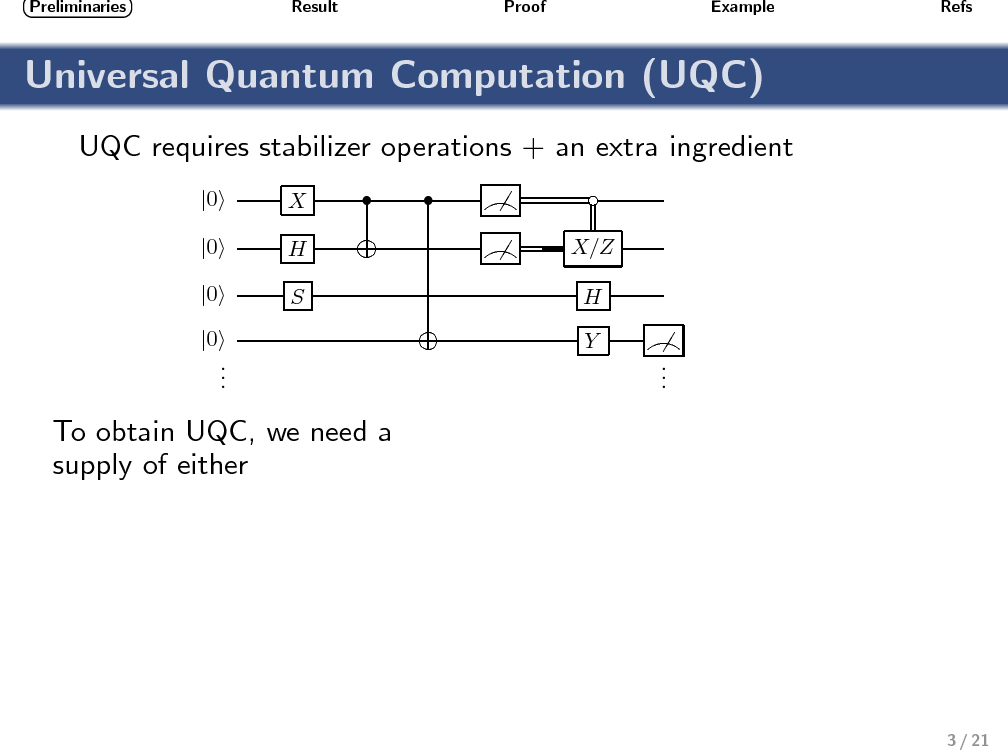
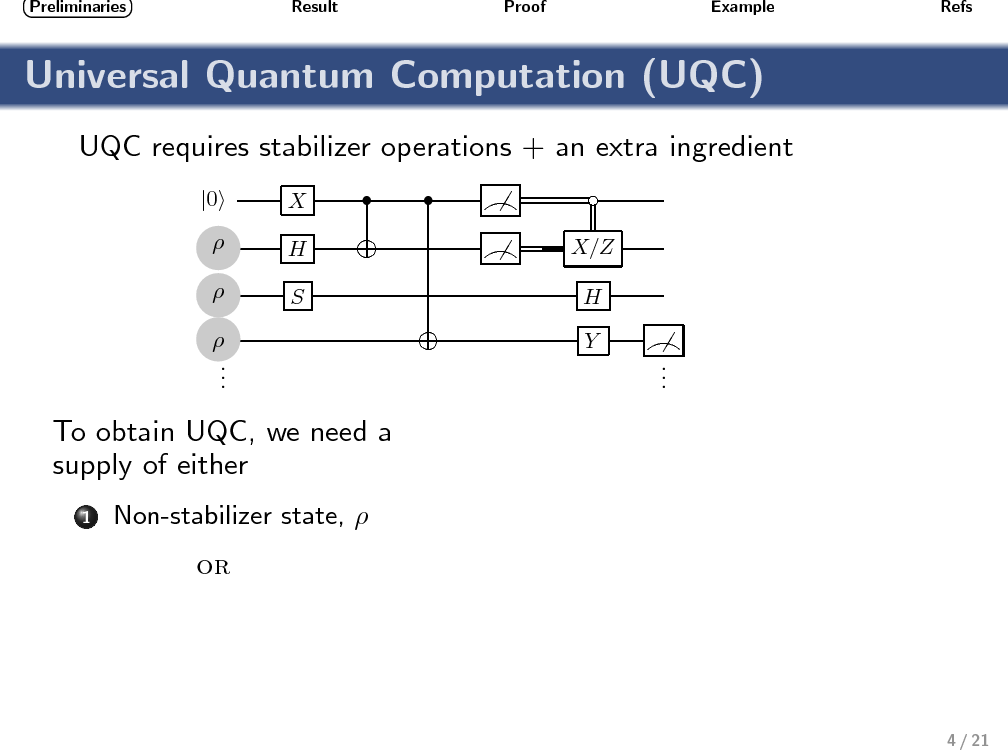
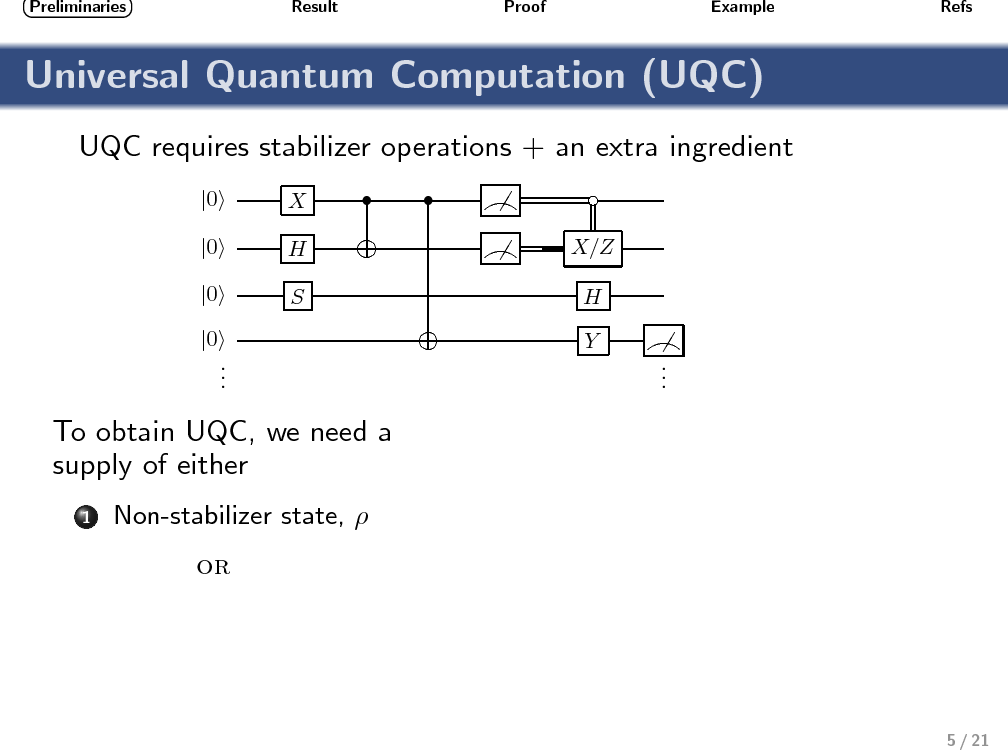
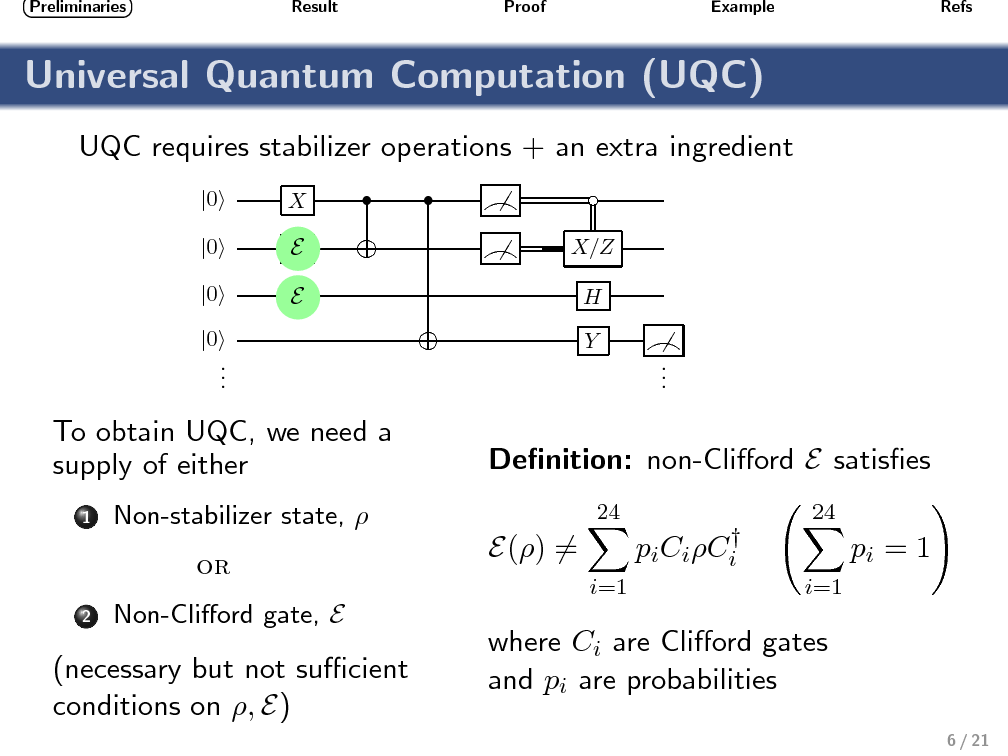
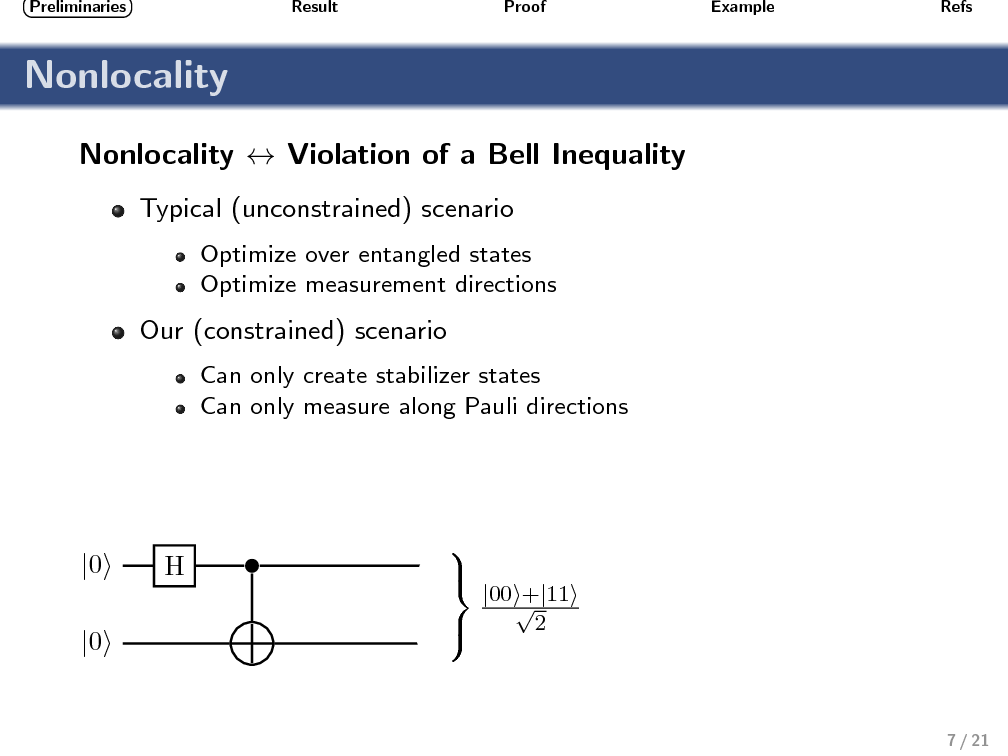
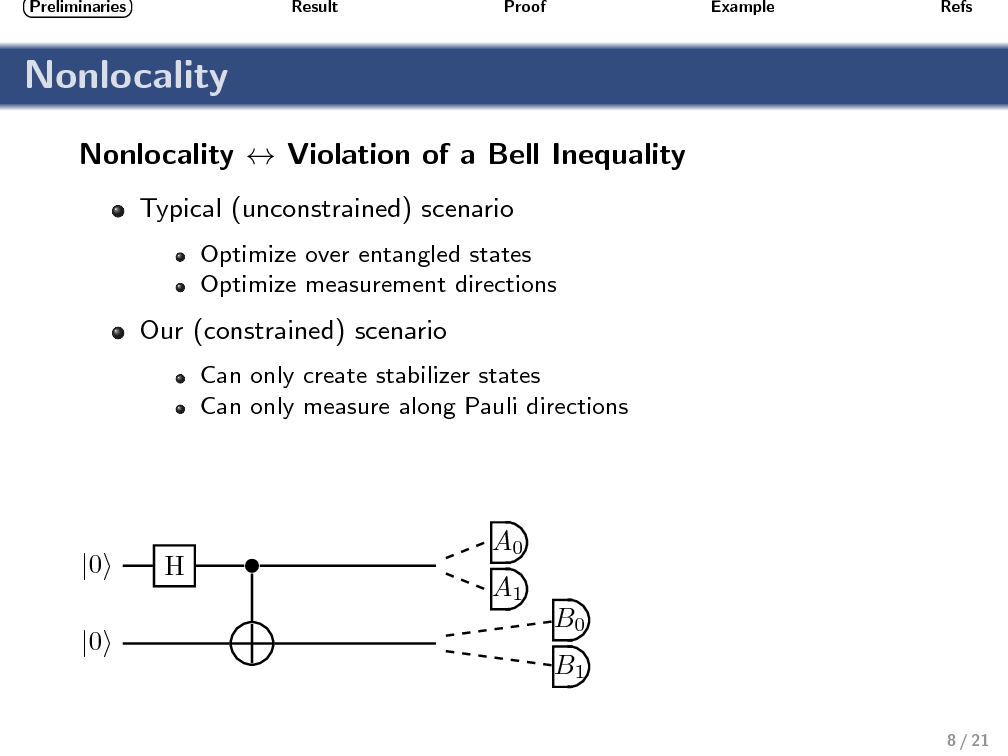
An obstacle affecting any proposal for a topological quantum computer based on Ising anyons is that quasiparticle braiding can only implement a finite (nonuniversal) set of quantum operations. The computational power of this restricted set of operations (often called stabilizer operations) has been studied in quantum information theory, and it is known that no quantum-computational advantage can be obtained without the help of an additional nonstabilizer operation. Similarly, a bipartite two-qubit system based on Ising anyons can not exhibit nonlocality (in the sense of violating a Bell inequality) when only topologically protected stabilizer operations are performed. To produce correlations that can not be described by a local hidden variable model again requires the use of a nonstabilizer operation. Using geometric techniques, we relate the sets of operations that enable universal quantum computing (UQC) with those that enable violation of a Bell inequality. Motivated by the fact that nonstabilizer operations are expected to be highly imperfect, our aim is to provide a benchmark for identifying UQC-enabling operations that is both experimentally practical and conceptually simple. We show that any (noisy) single-qubit nonstabilizer operation that, together with perfect stabilizer operations, enables violation of the simplest two-qubit Bell inequality, can also be used to enable UQC. This benchmarking requires finding the expectation values of two distinct Pauli measurements on each qubit of a bipartite system.