Qudit versions of the qubit T gate
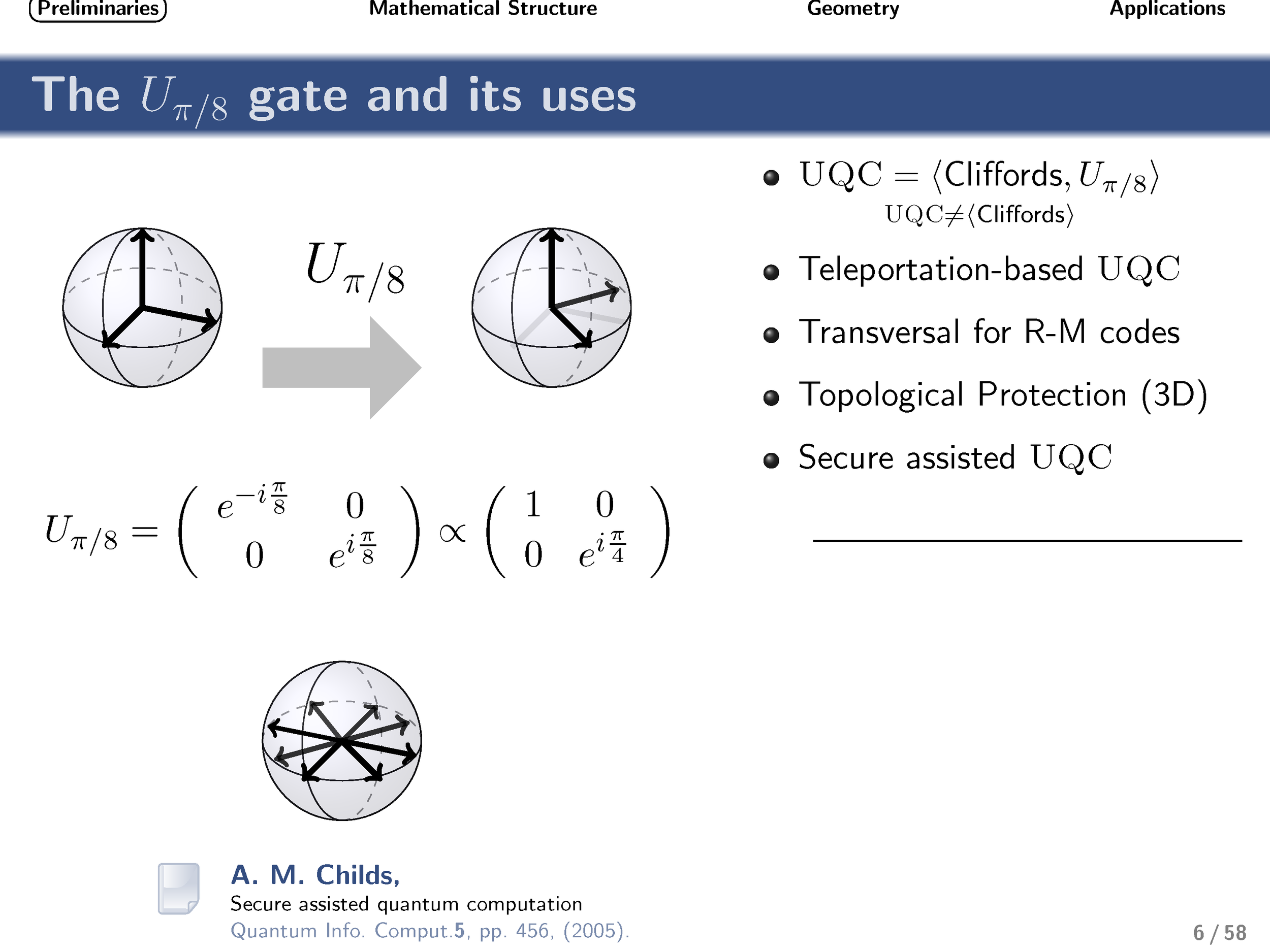
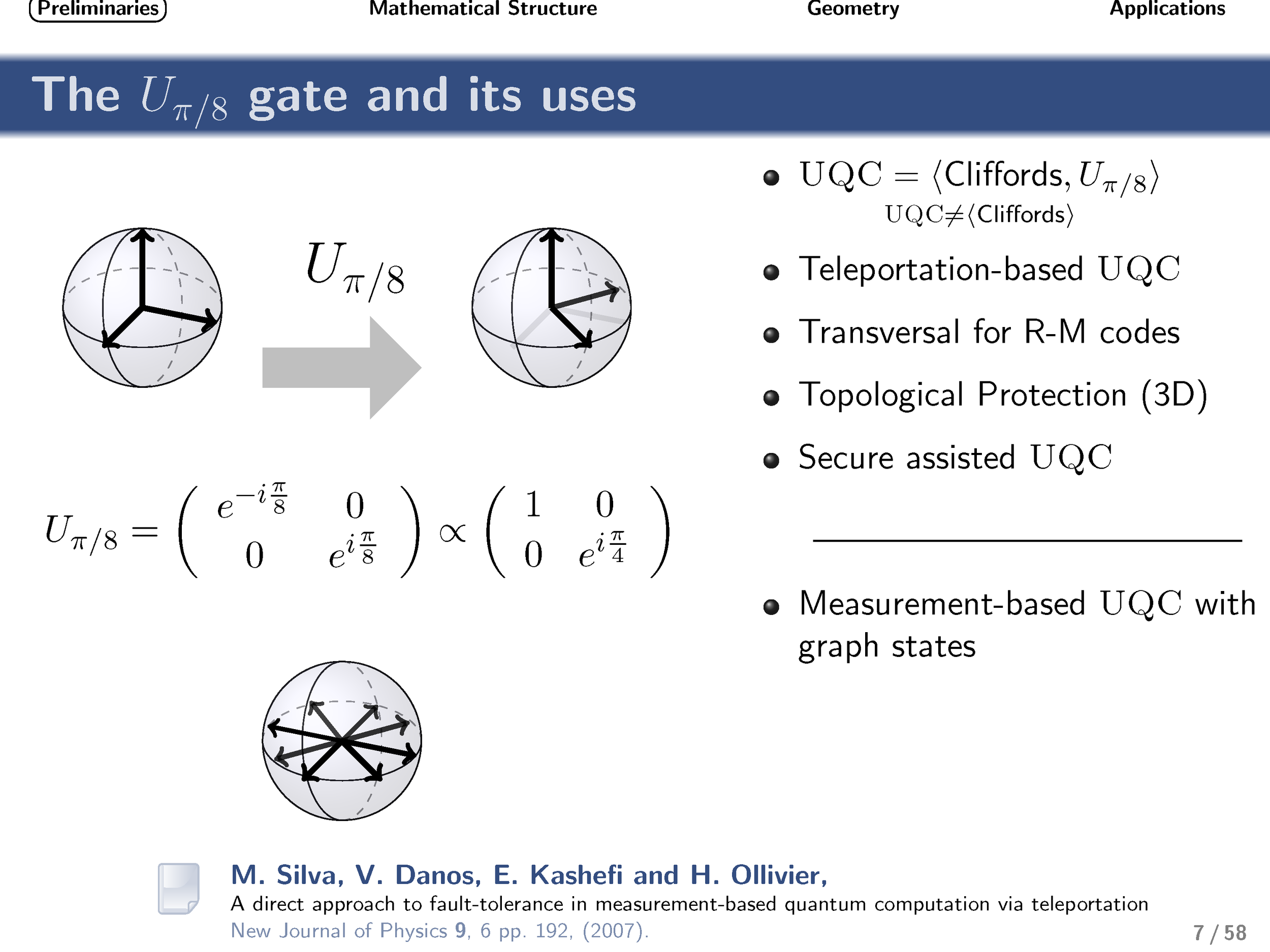
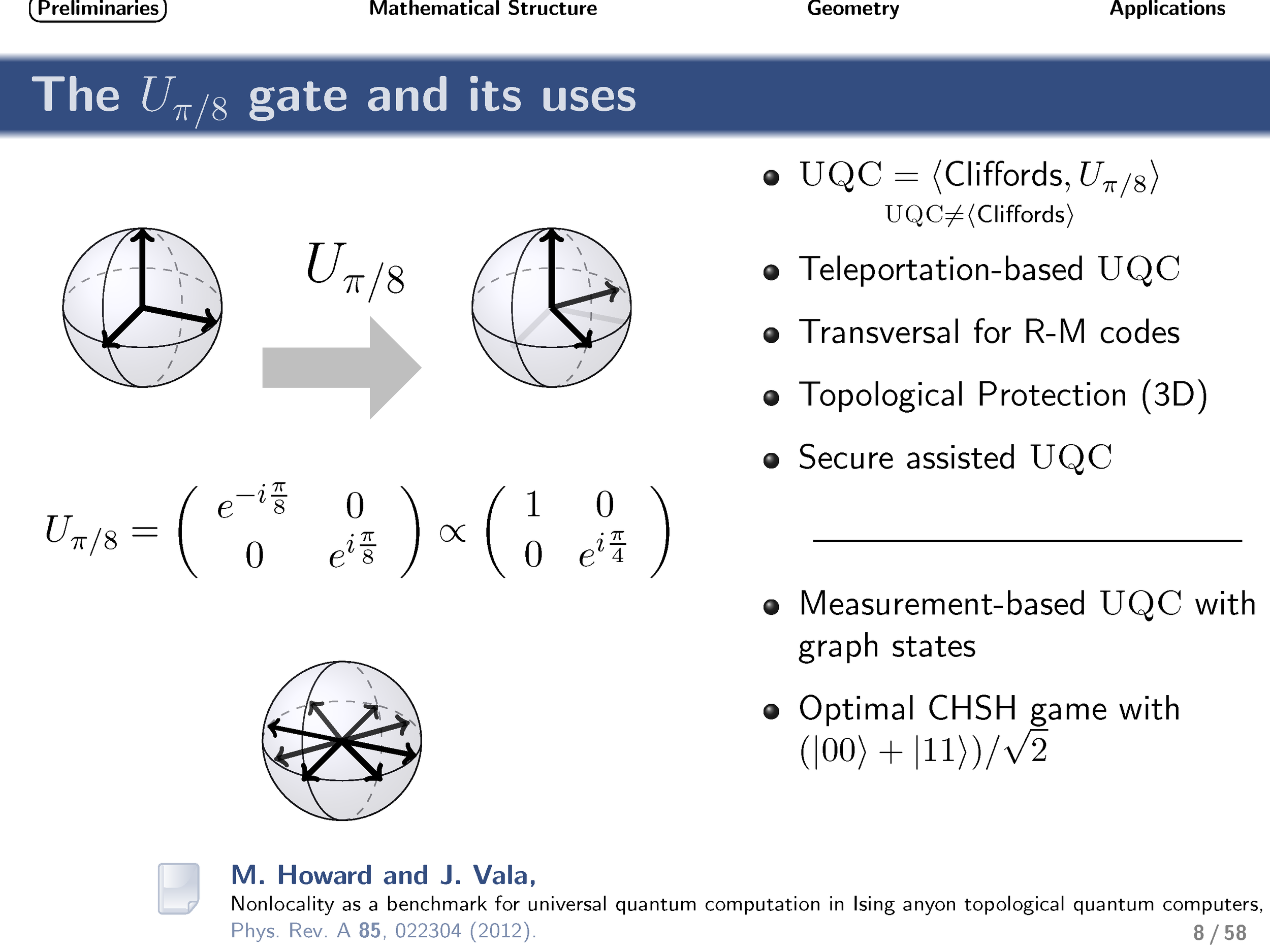
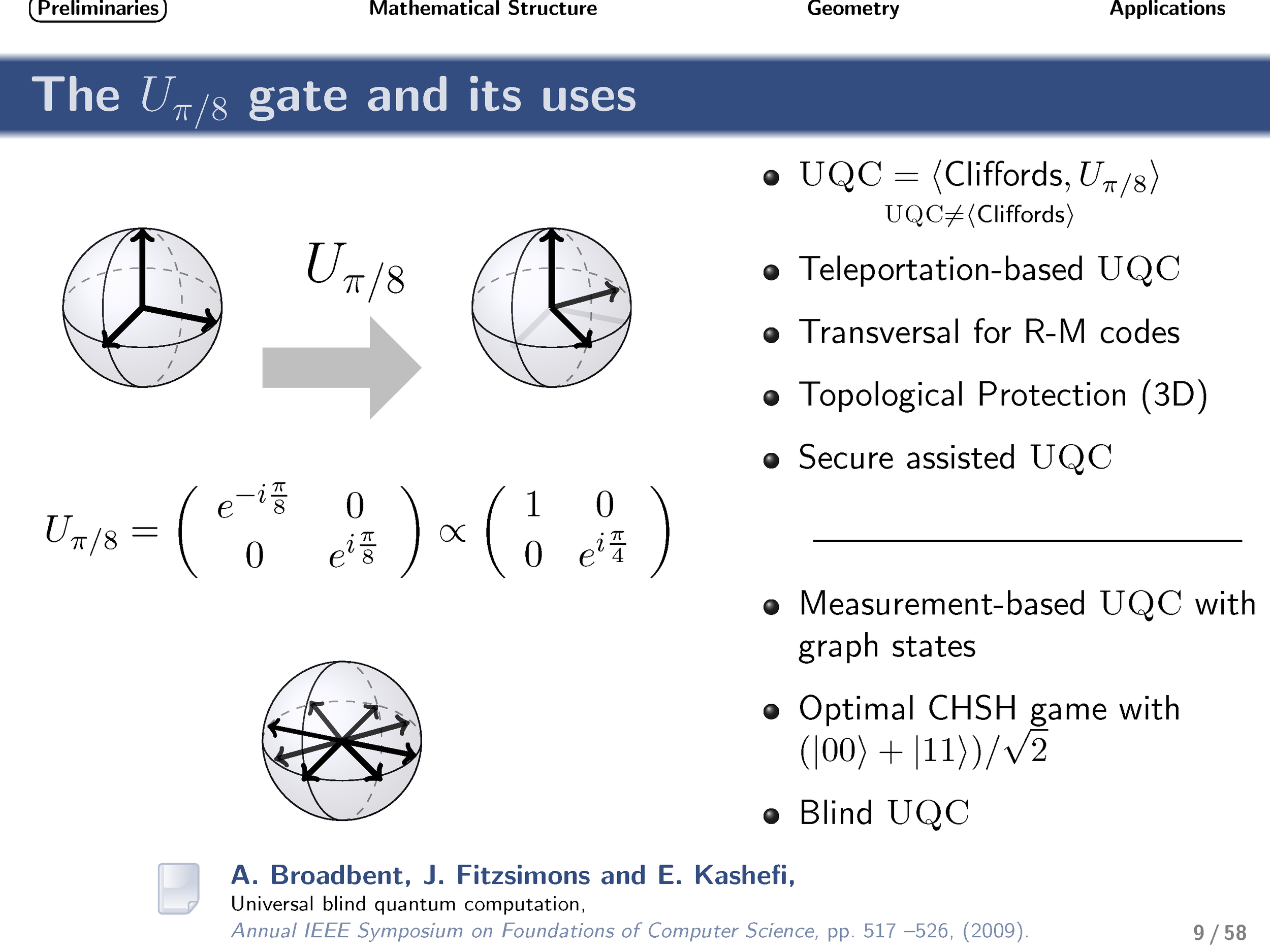
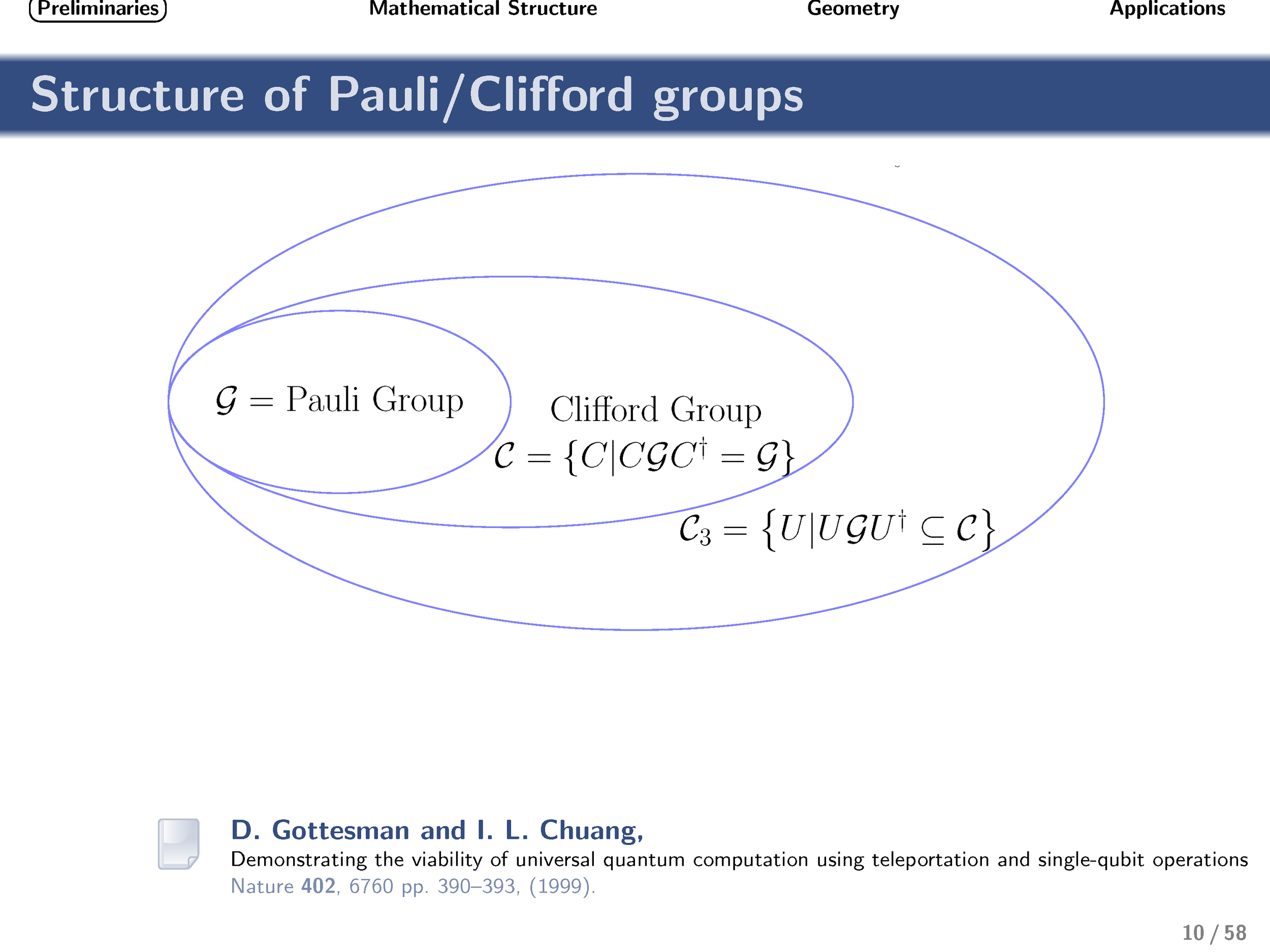
When visualized as an operation on the Bloch sphere, the qubit π/8 gate corresponds to 1/8 of a complete rotation about the vertical axis. This simple gate often plays an important role in quantum information theory, typically in situations for which Pauli and Clifford gates are insufficient. Most notably, if it supplements the set of Clifford gates, then universal quantum computation can be achieved. The π/8 gate is the simplest example of an operation from the third level of the Clifford hierarchy (i.e., it maps Pauli operations to Clifford operations under conjugation).
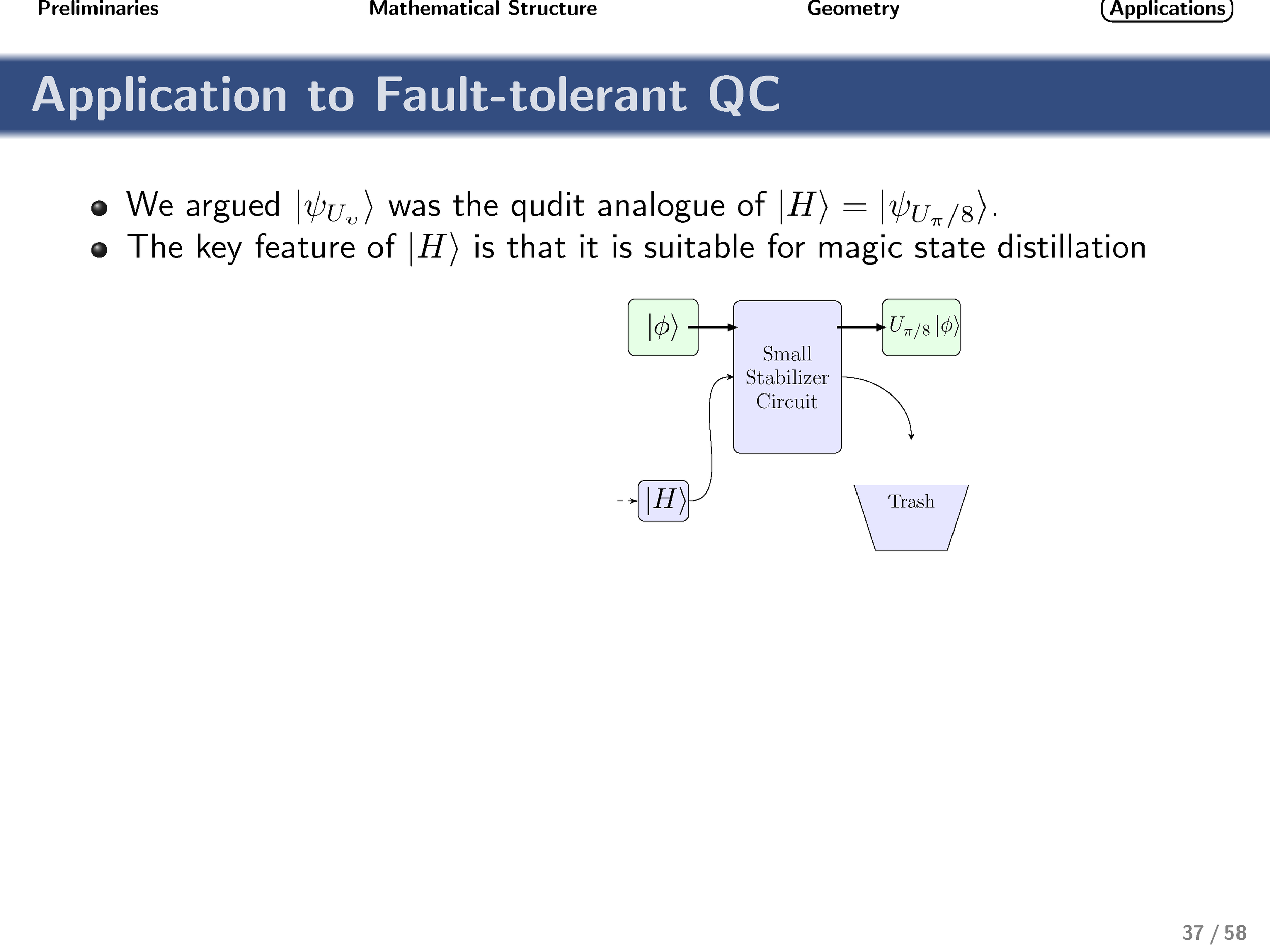
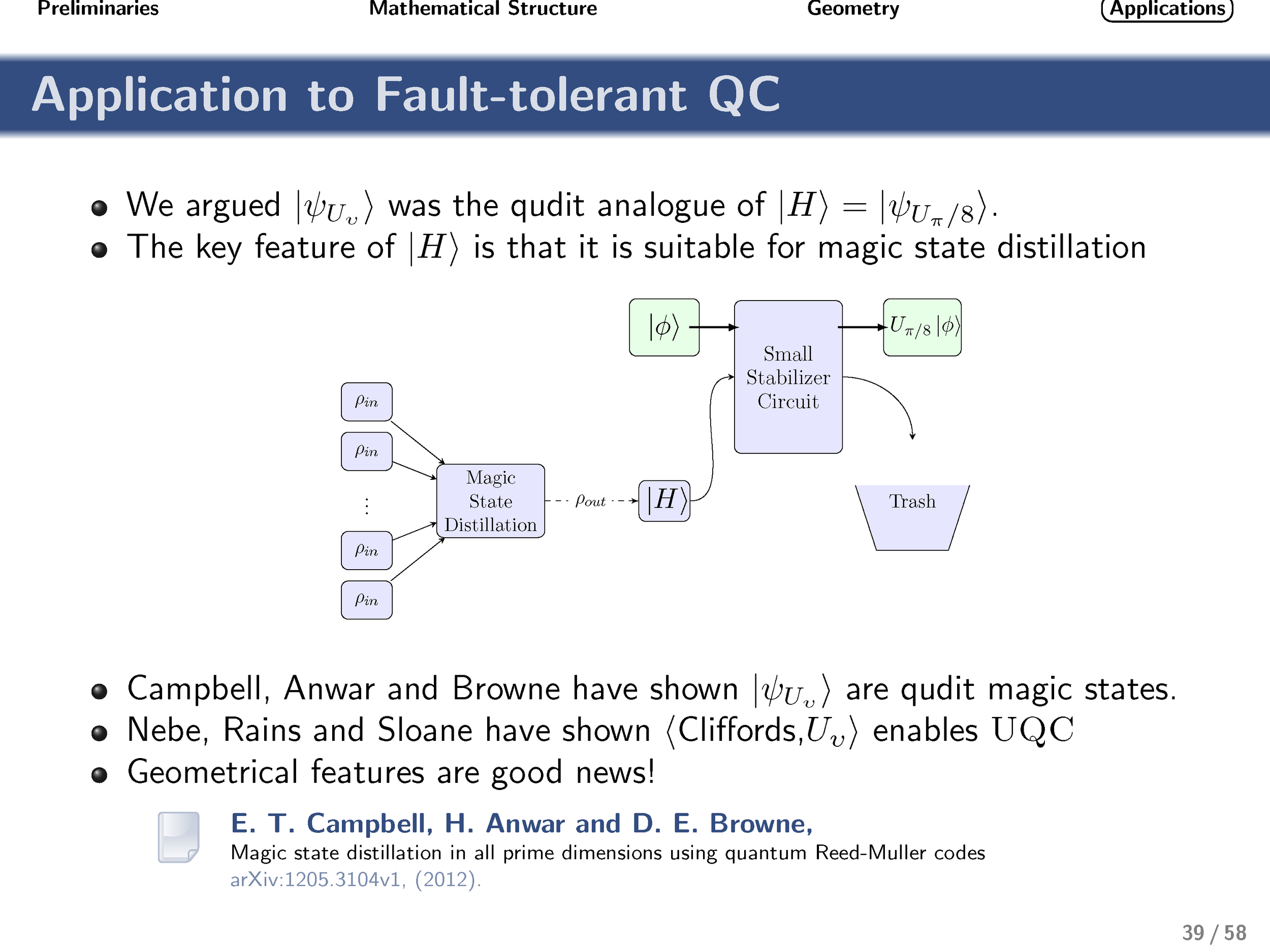
Here we derive explicit expressions for all qudit (d-level, where d is prime) versions of this gate and analyze the resulting group structure that is generated by these diagonal gates. This group structure differs depending on whether the dimensionality of the qudit is two, three, or greater than three. We then discuss the geometrical relationship of these gates (and associated states) with respect to Clifford gates and stabilizer states. We present evidence that these gates are maximally robust to depolarizing and phase-damping noise, in complete analogy with the qubit case. Motivated by this and other similarities, we conjectured that these gates could be useful for the task of qudit magic-state distillation and, by extension, fault-tolerant quantum computing. Very recently, independent work by Campbell et al. confirmed the correctness of this intuition, and we build upon their work to characterize noise regimes for which noisy implementations of these gates can (or provably cannot) supplement Clifford gates to enable universal quantum computation.
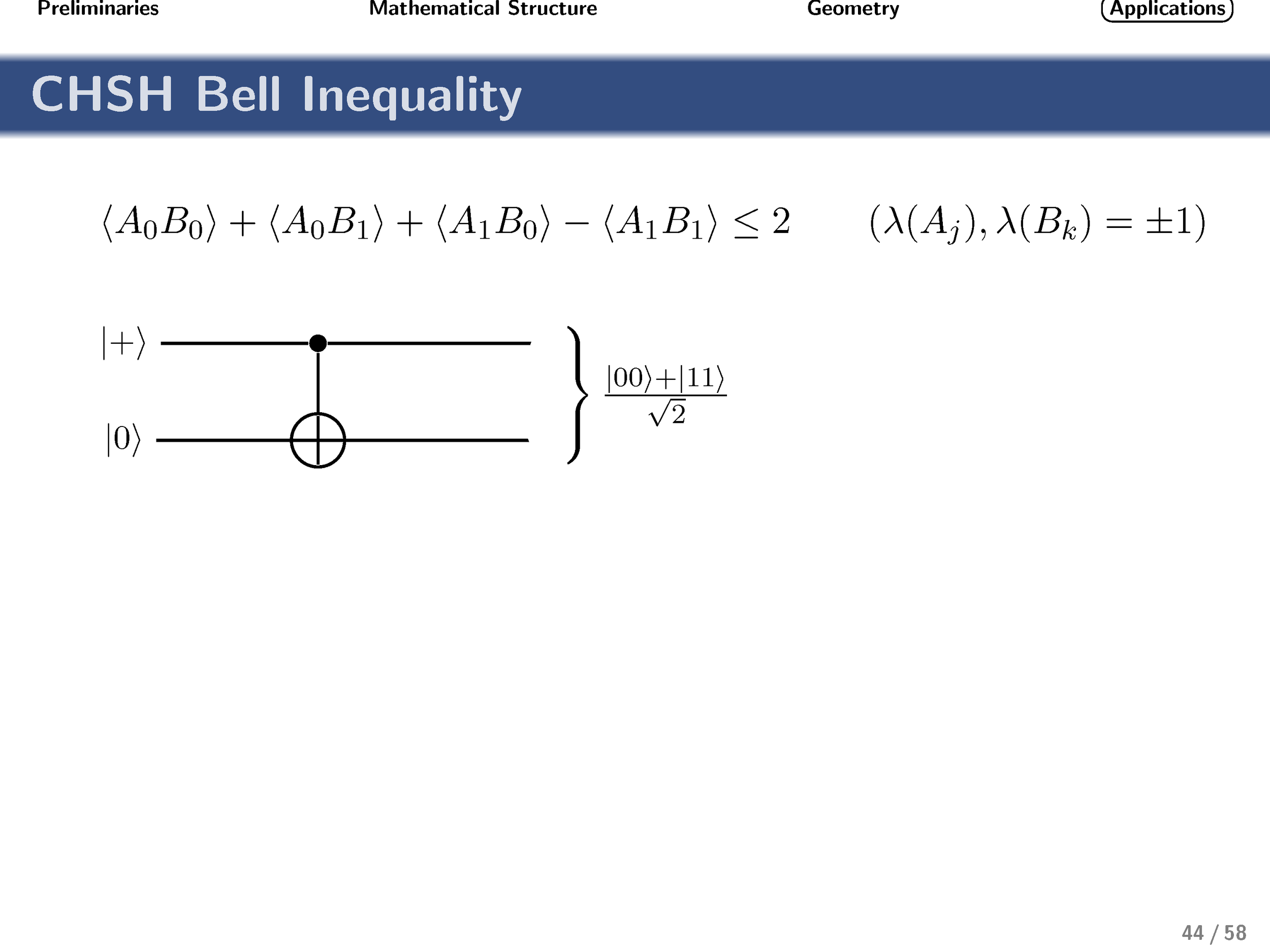
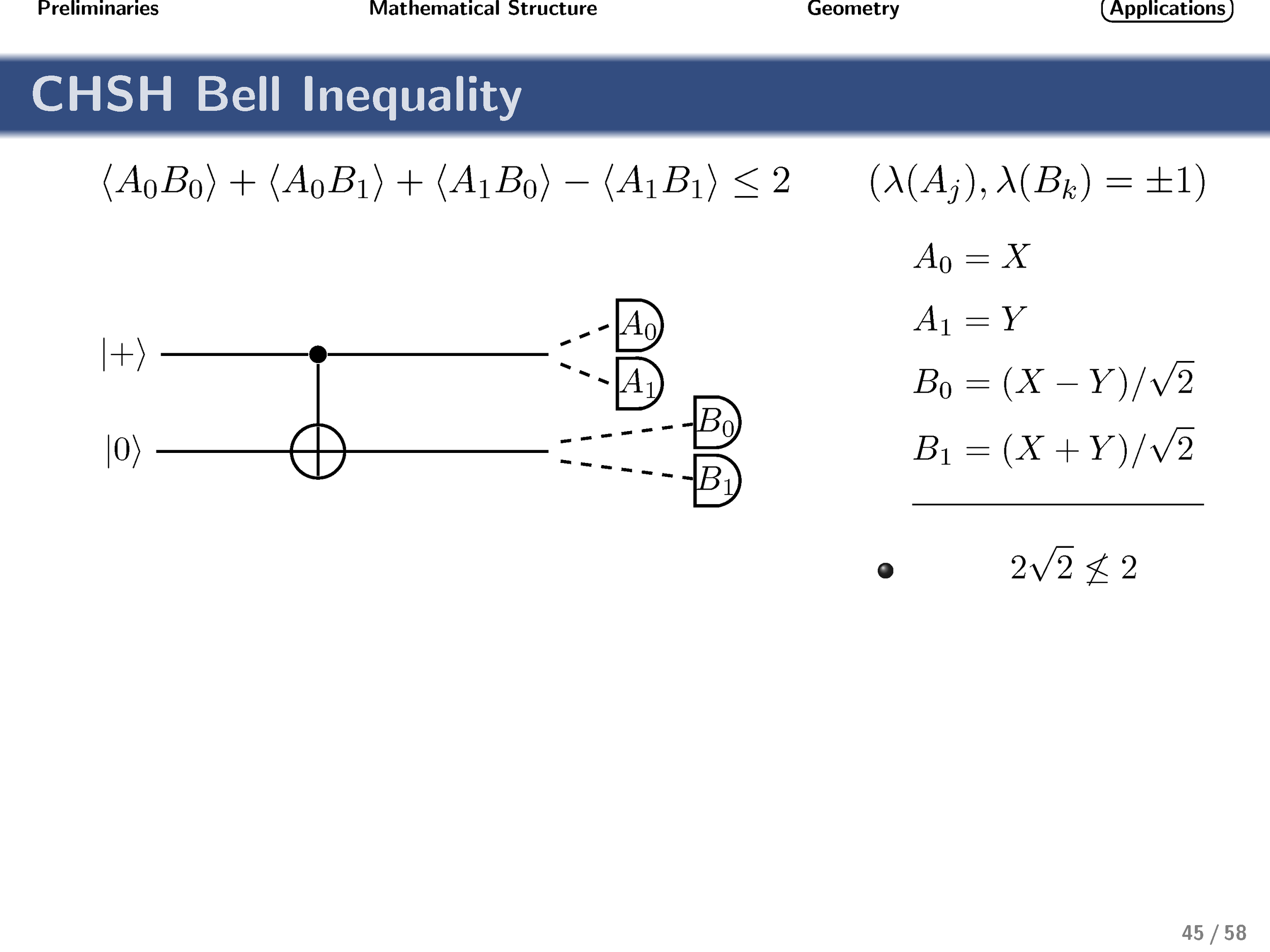
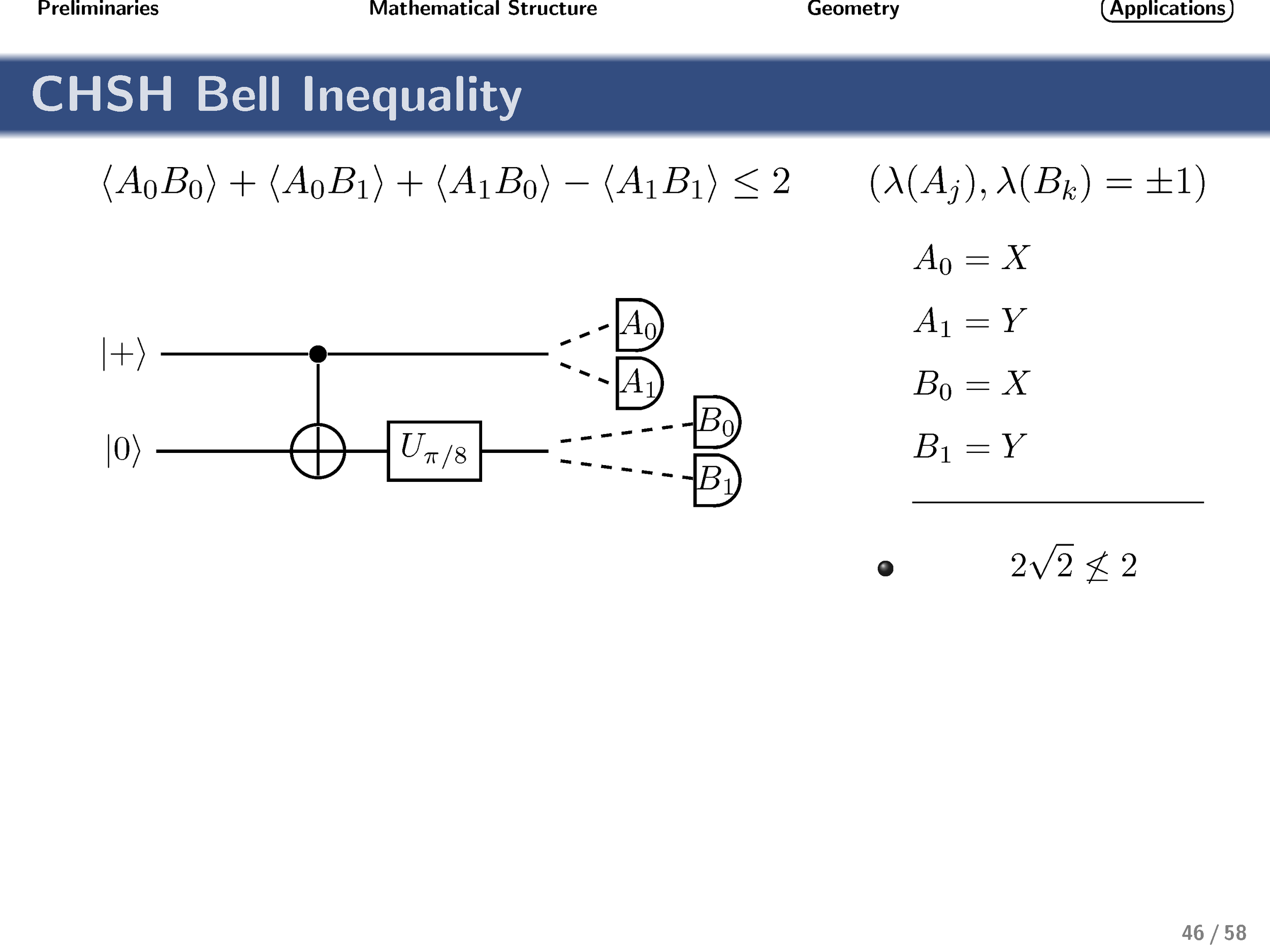
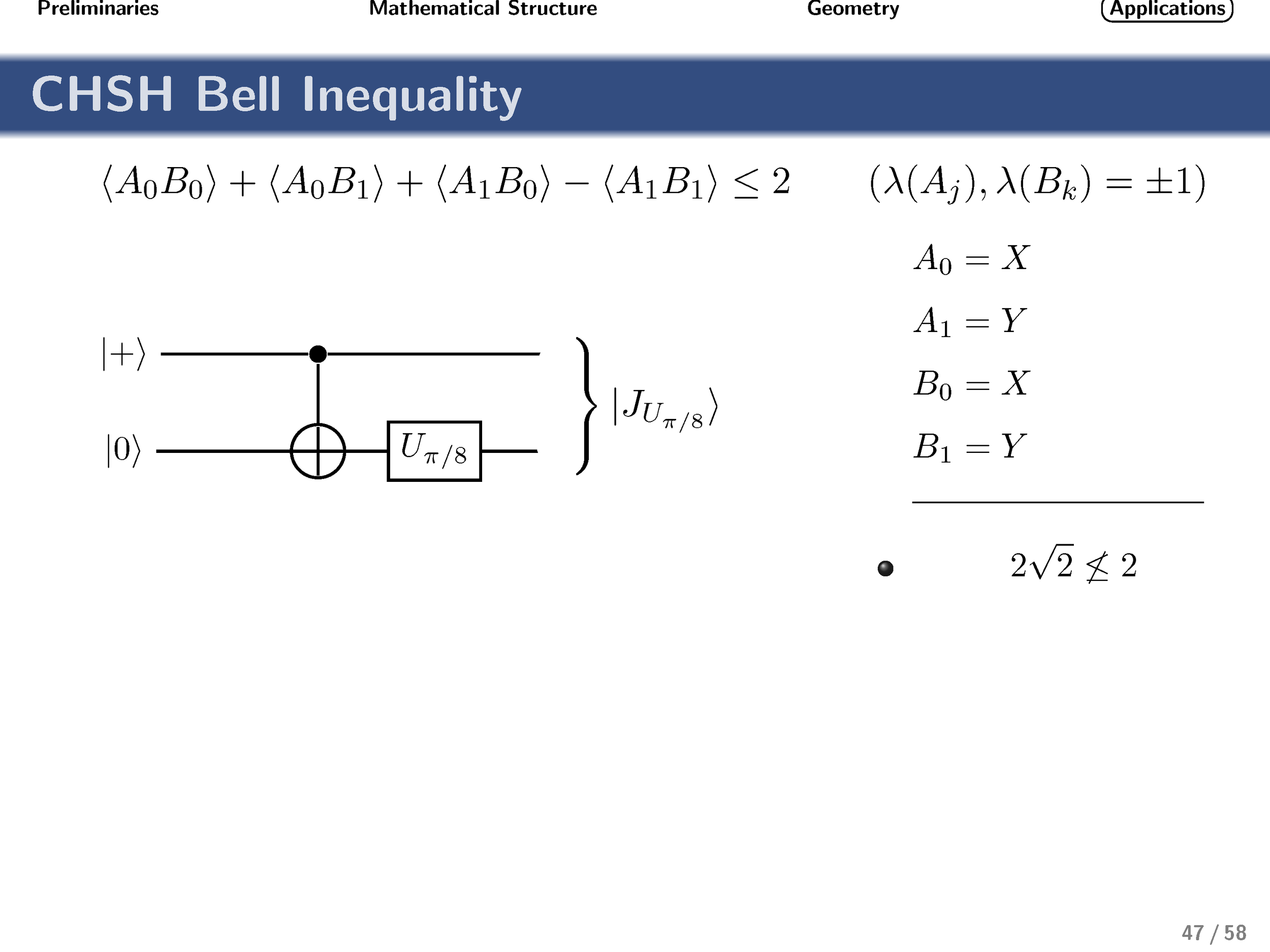
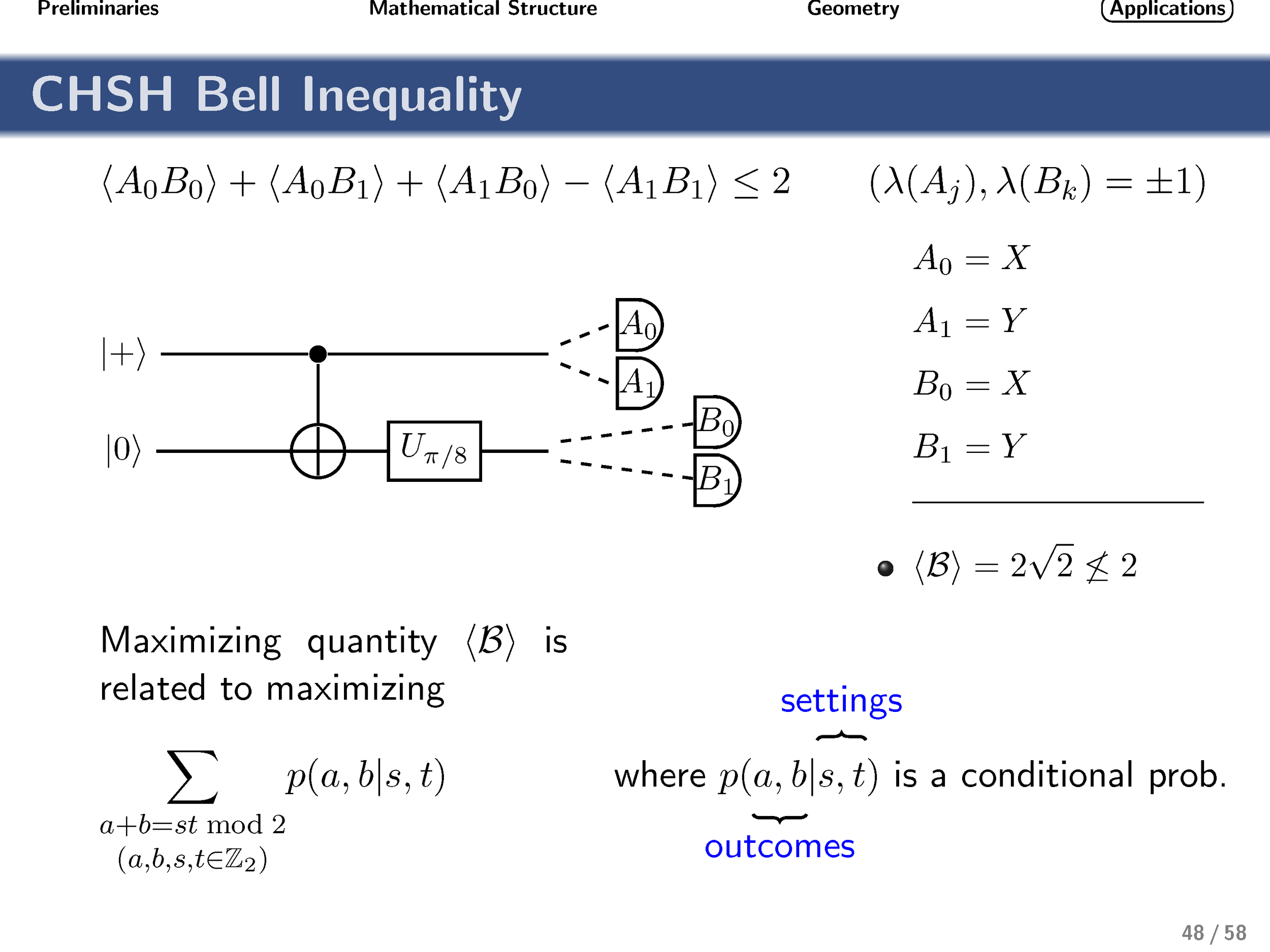
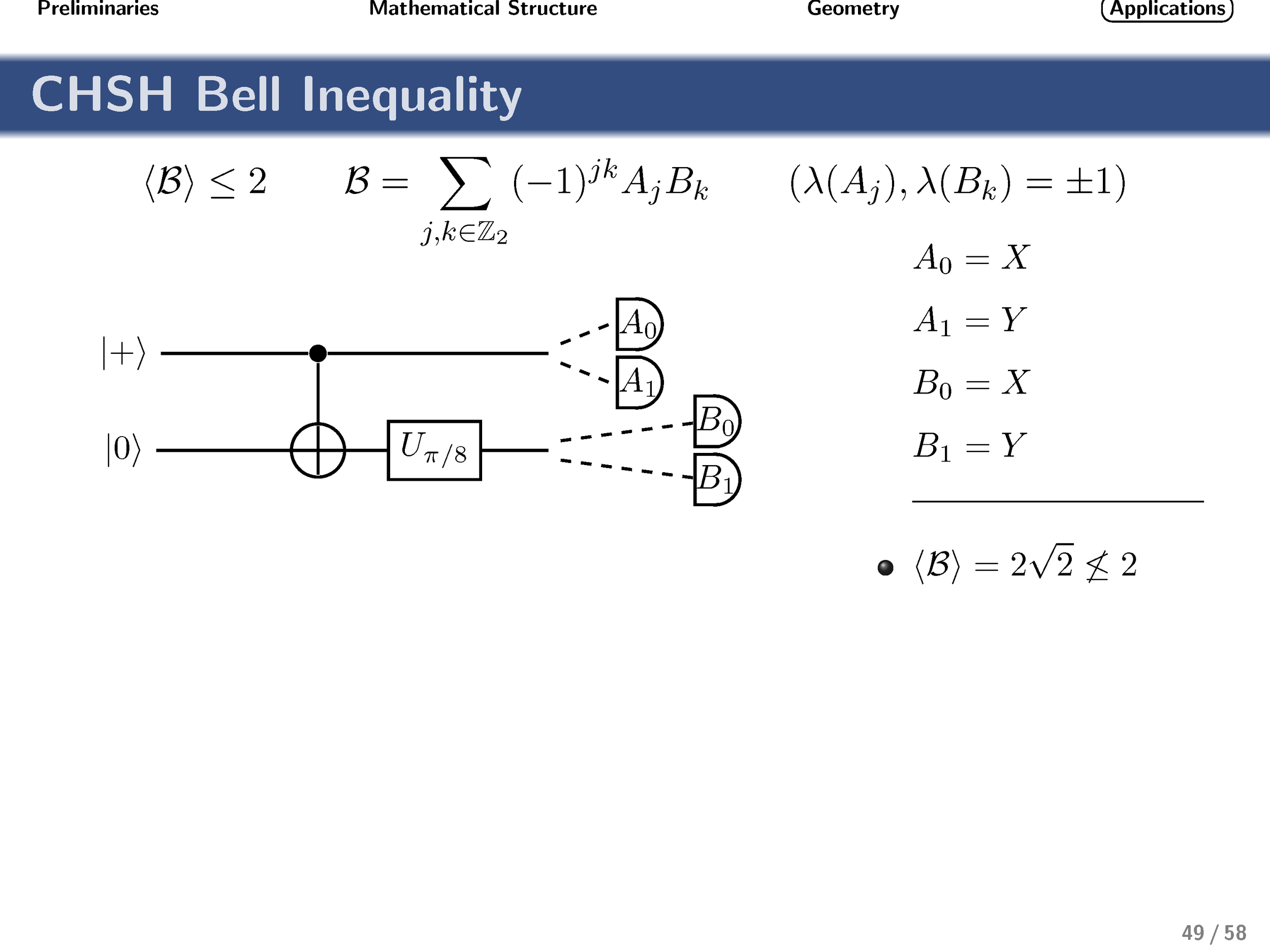
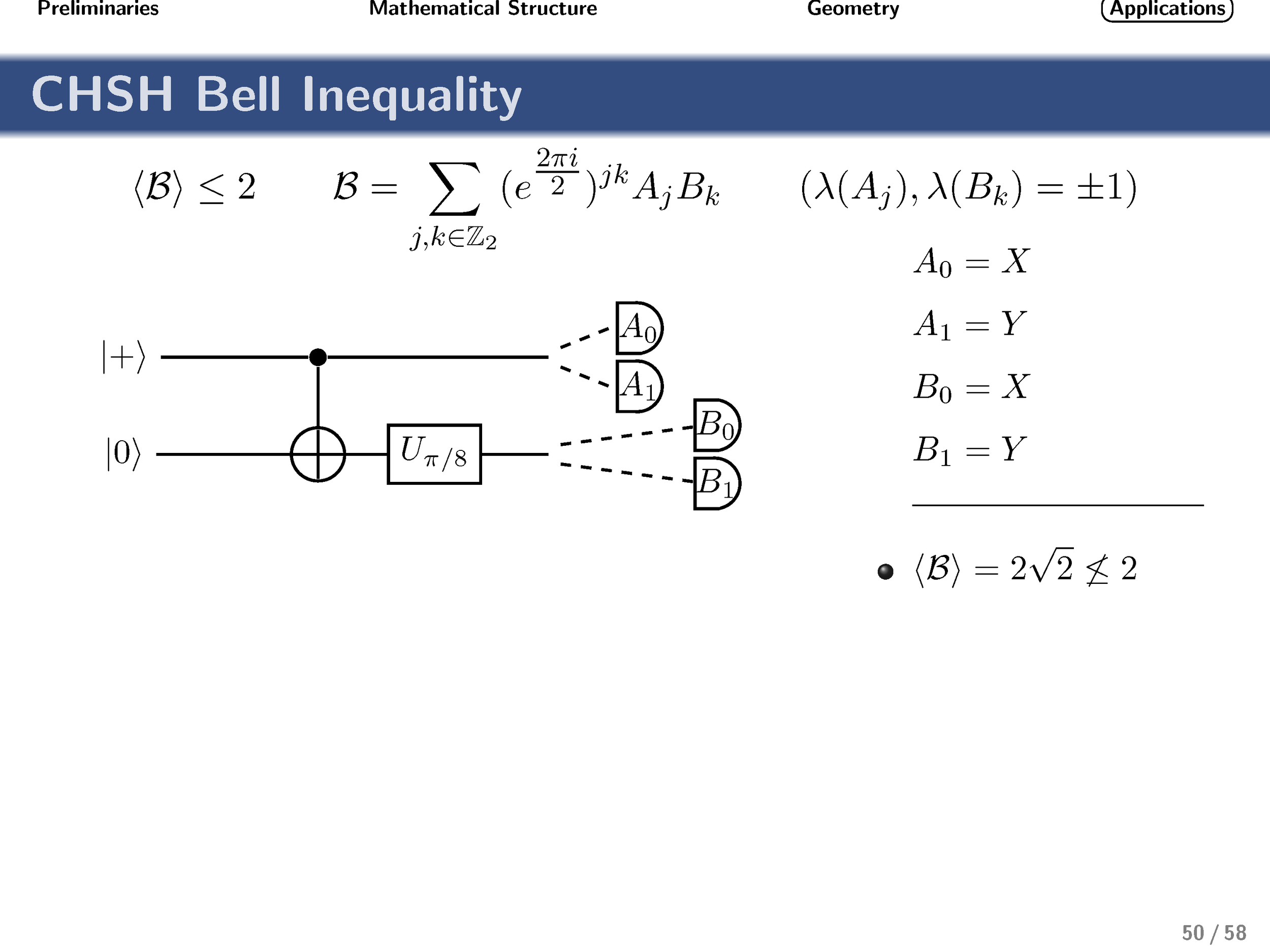
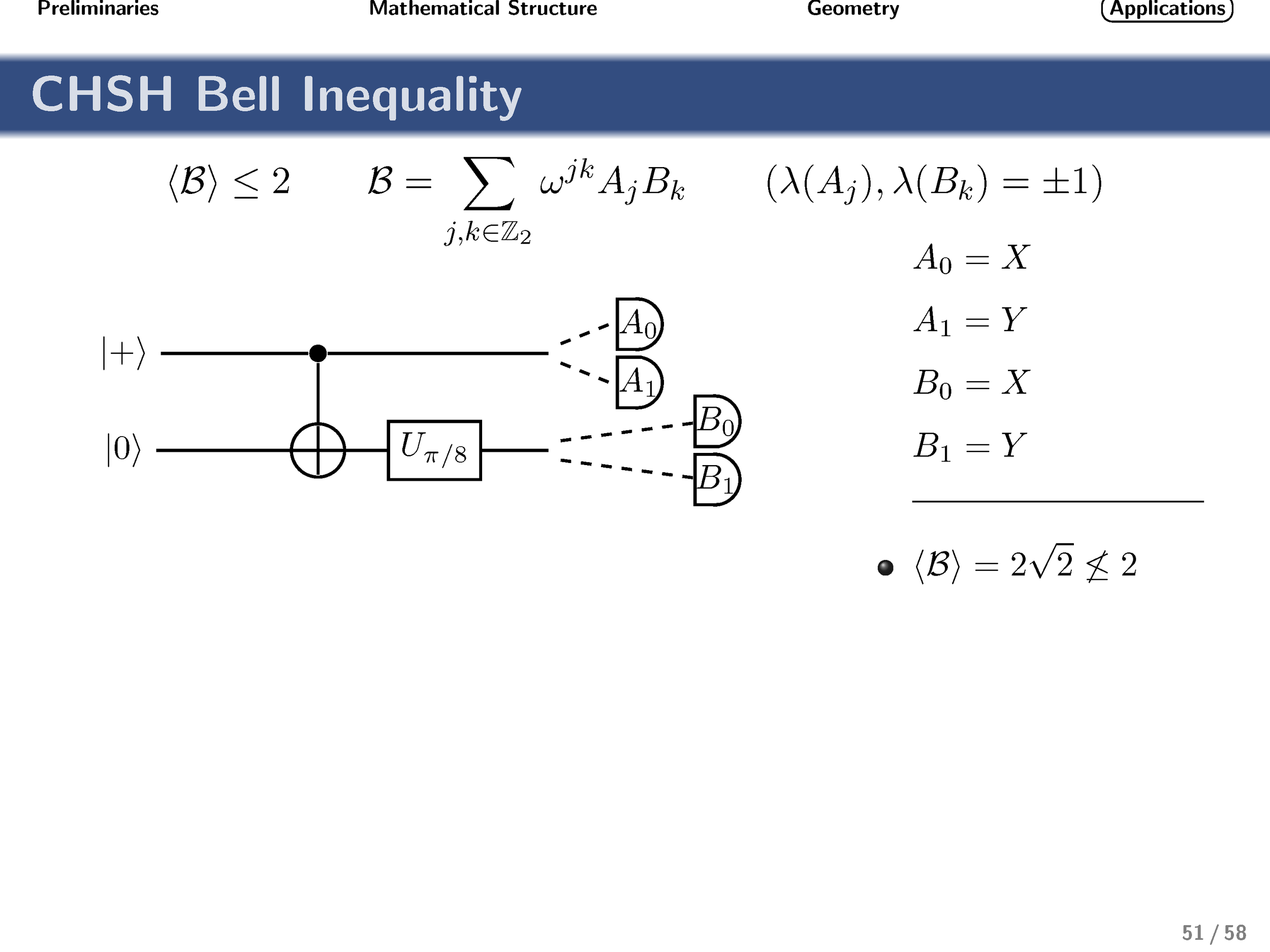
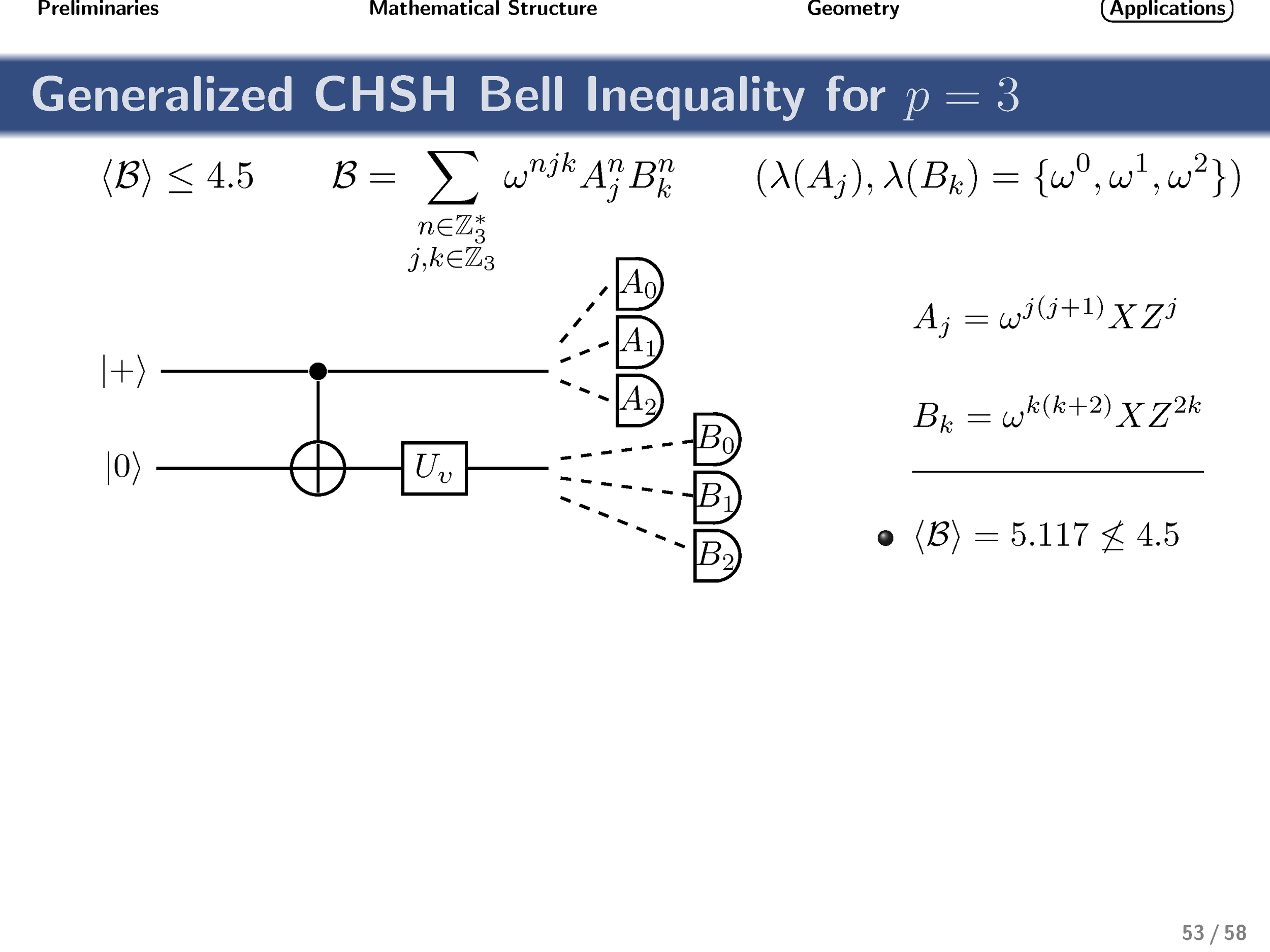
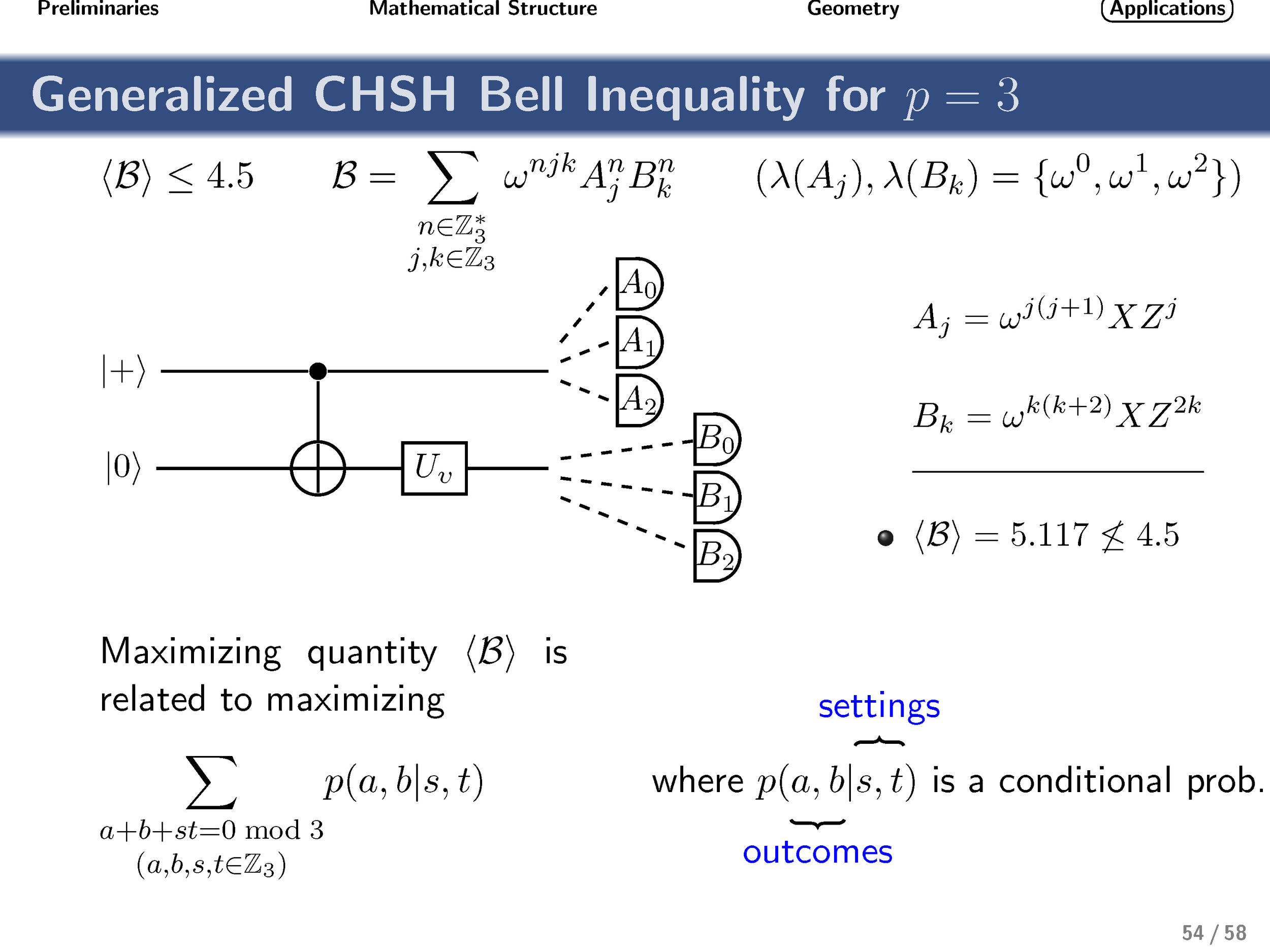
Finally, turning our attention to nonlocality, we show that these gates achieve the optimal quantum strategy for the generalized qudit CHSH inequality.