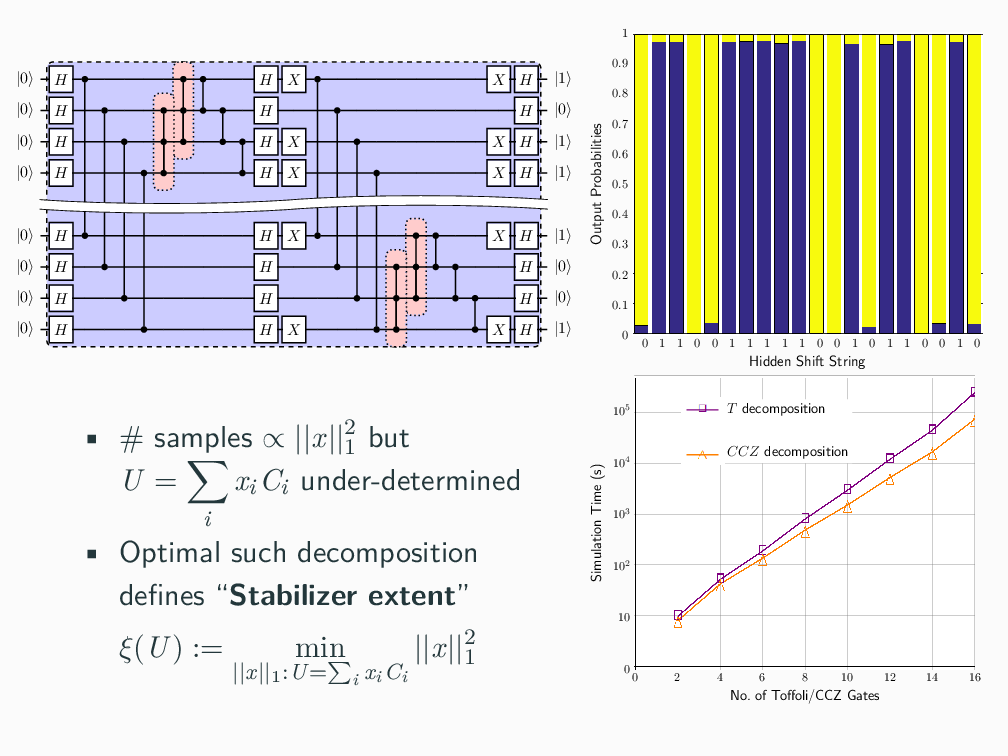
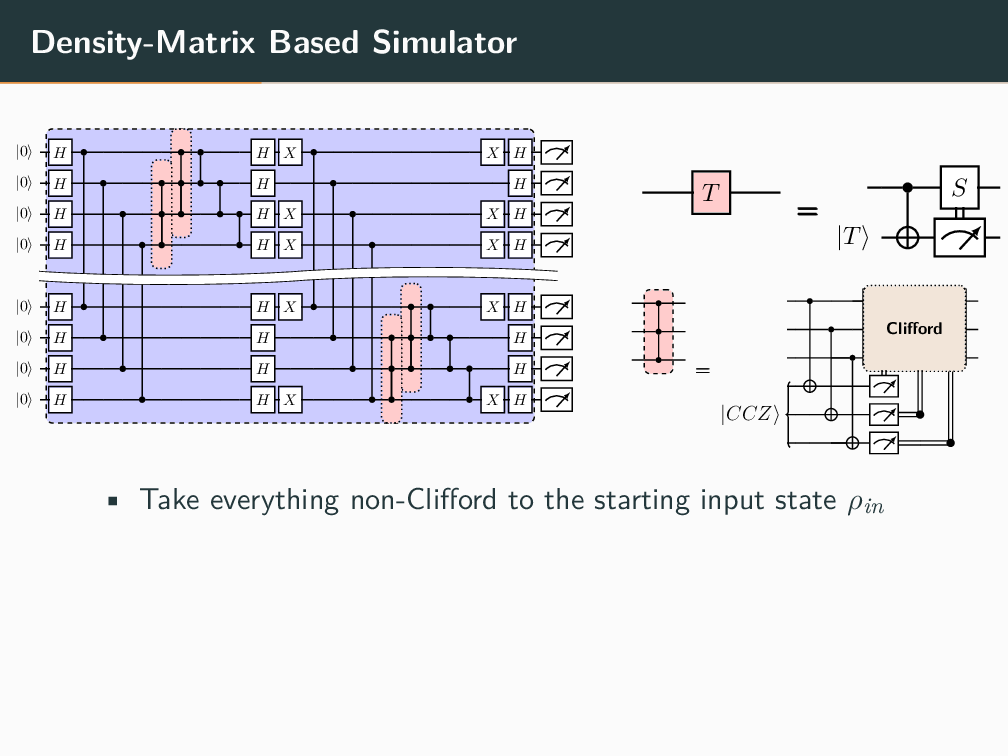
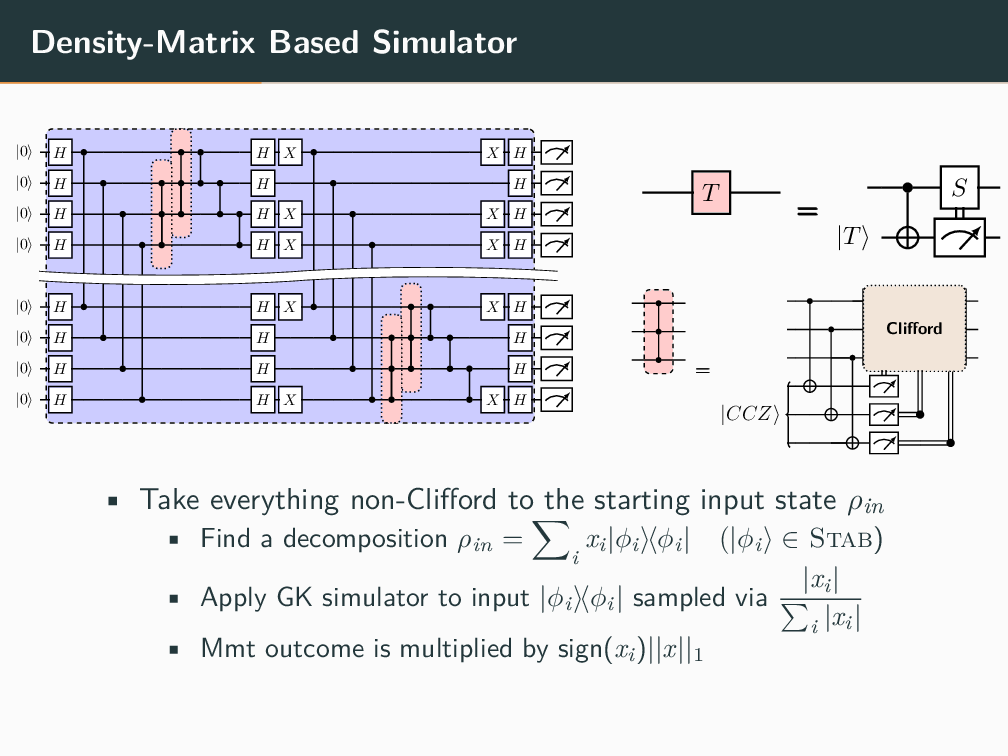
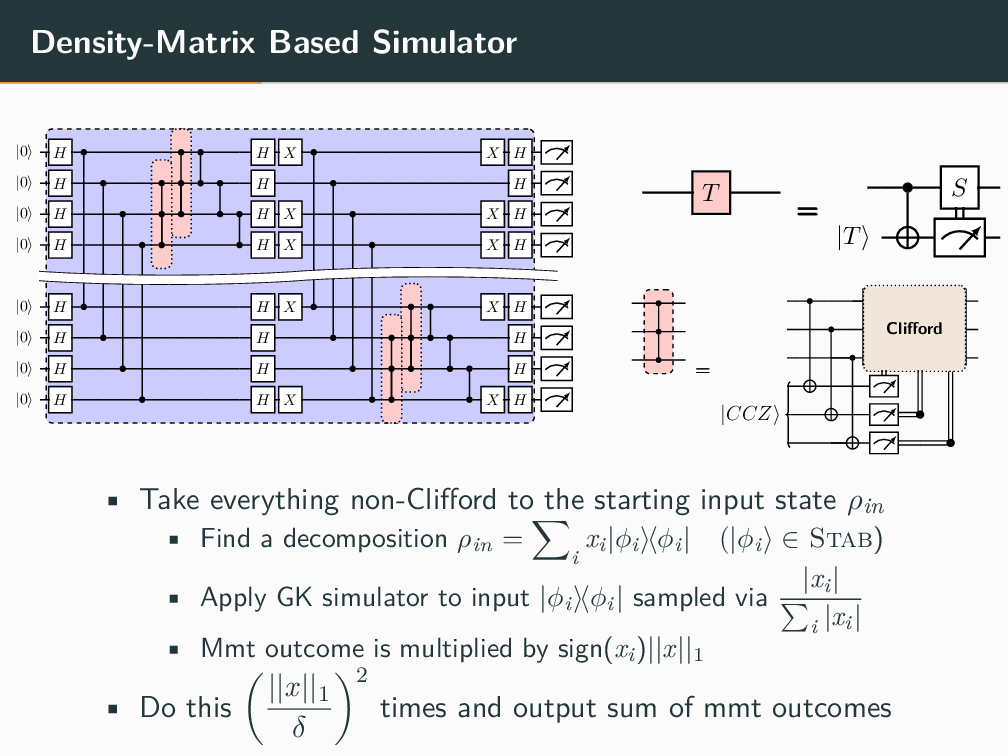
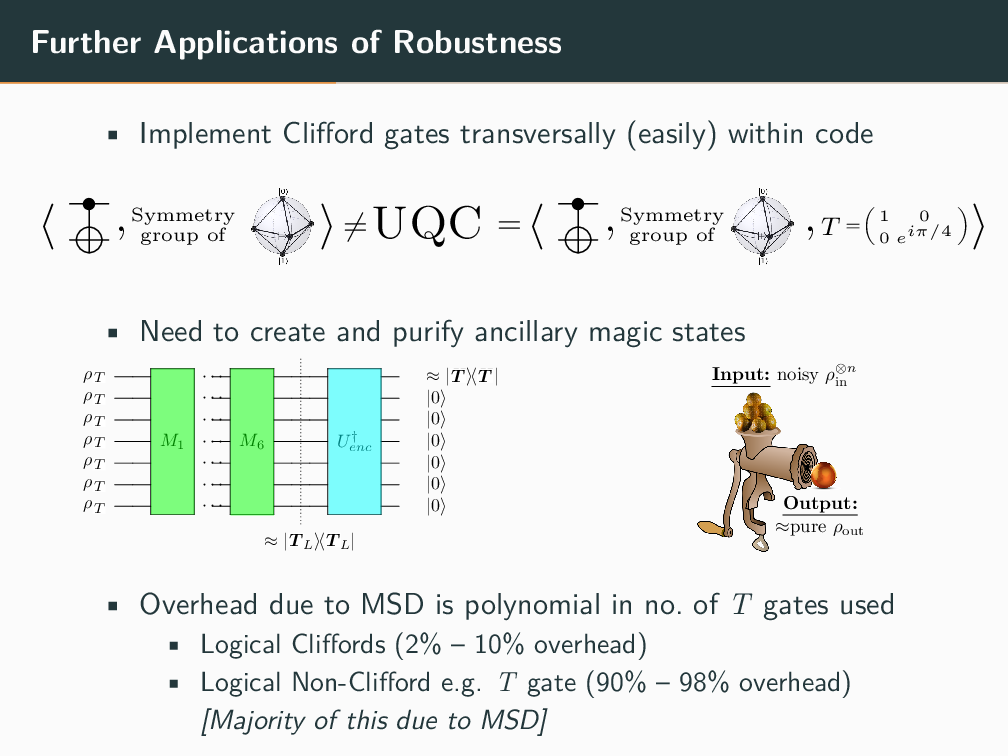
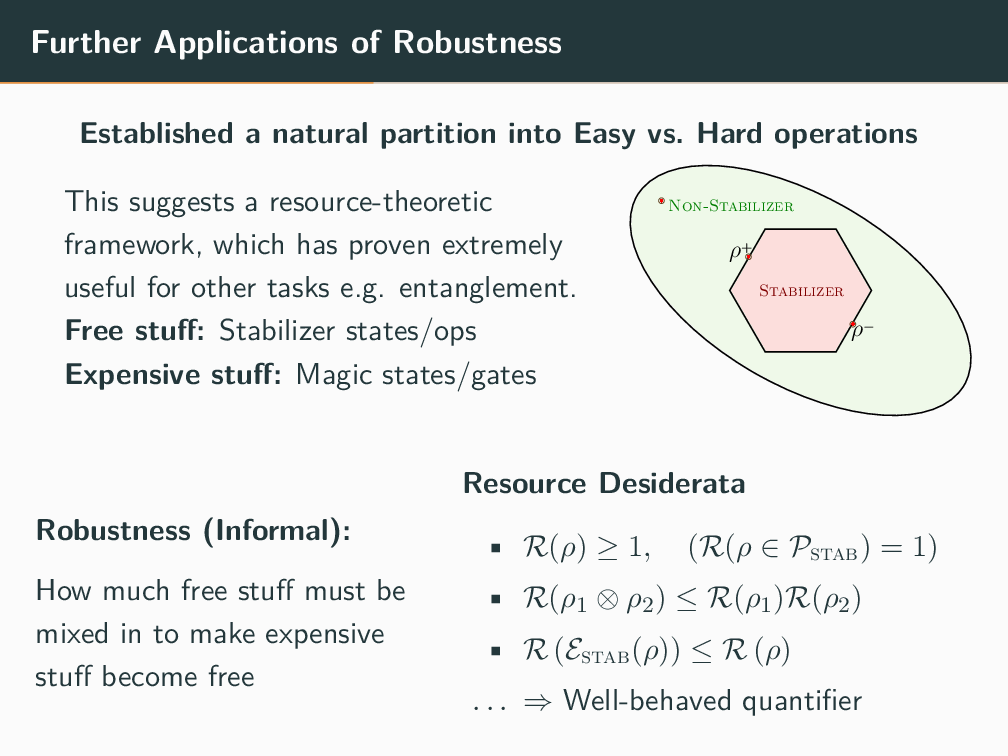
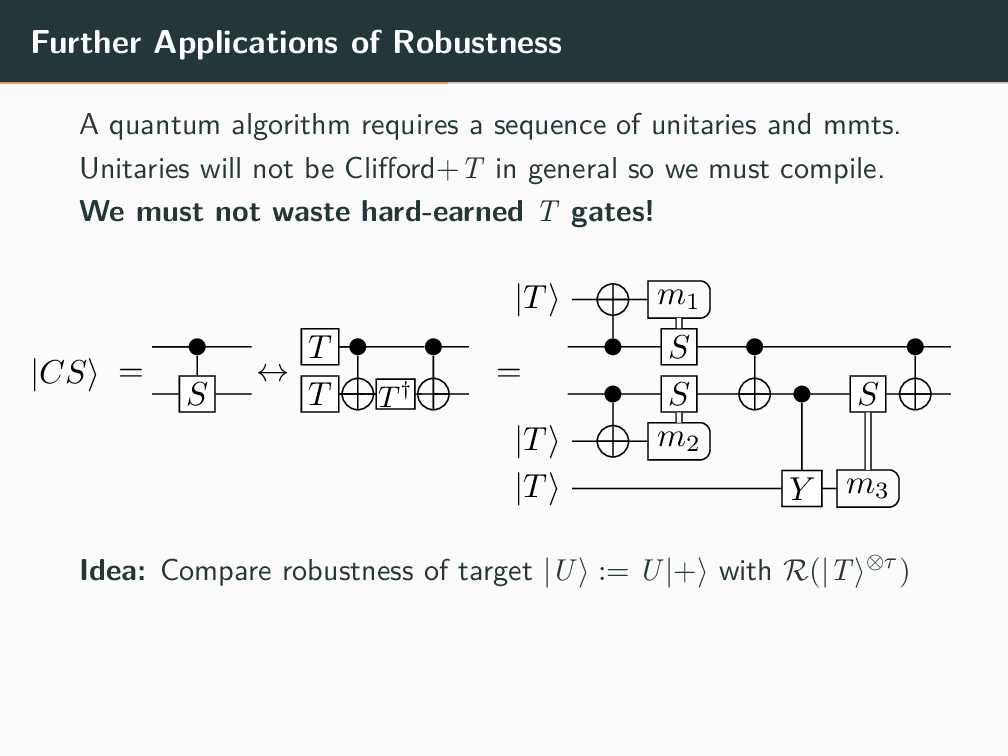
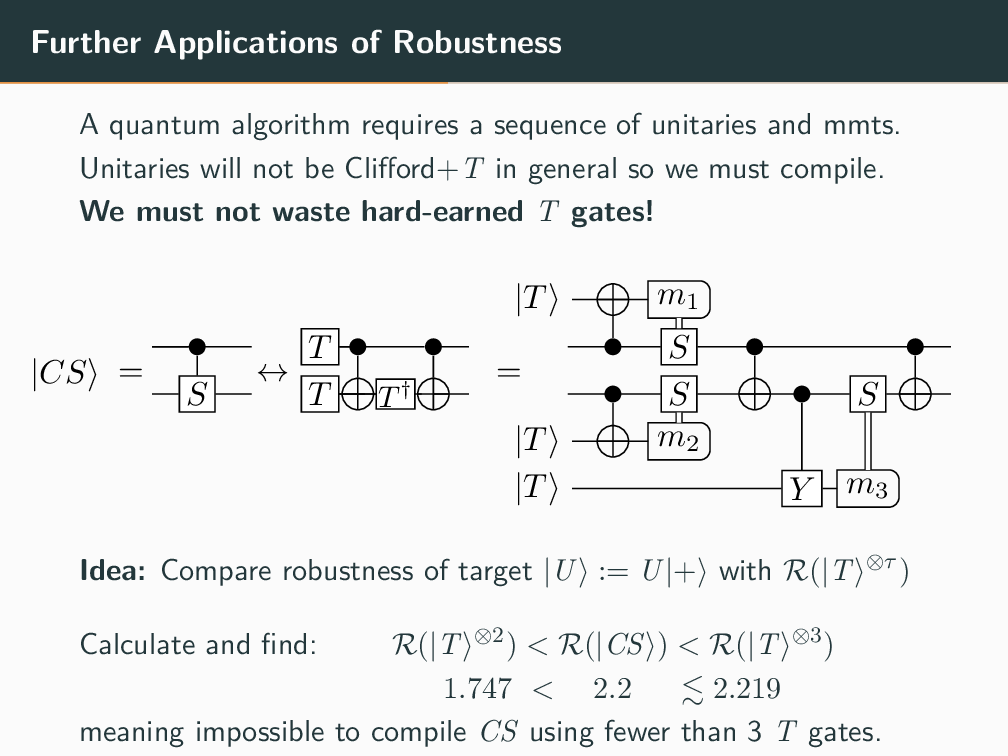
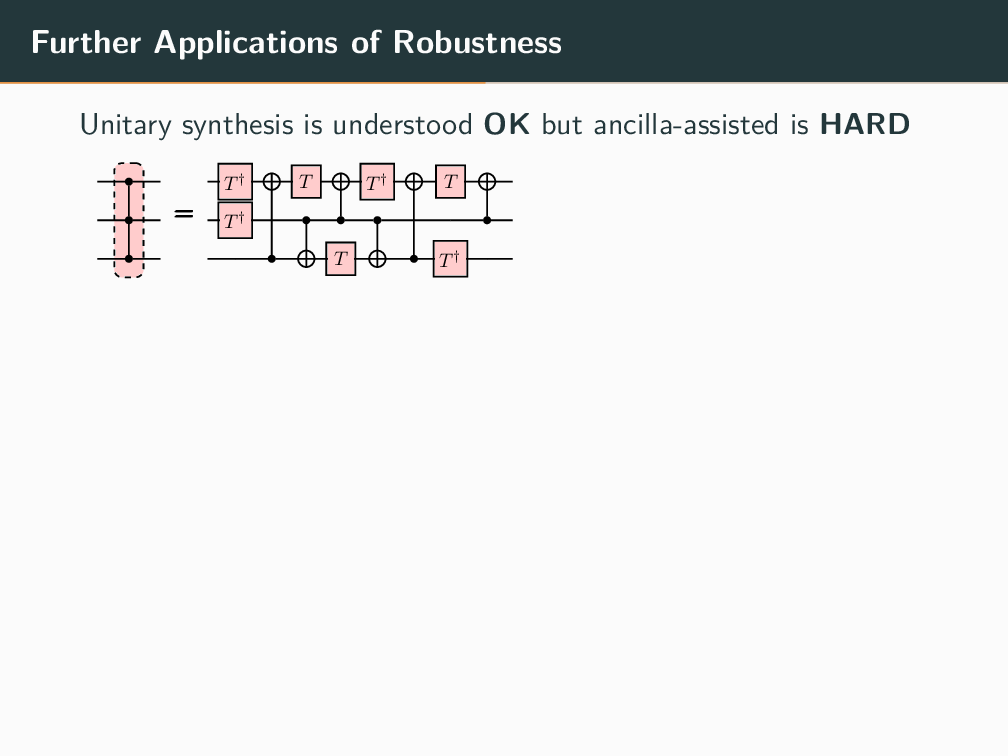
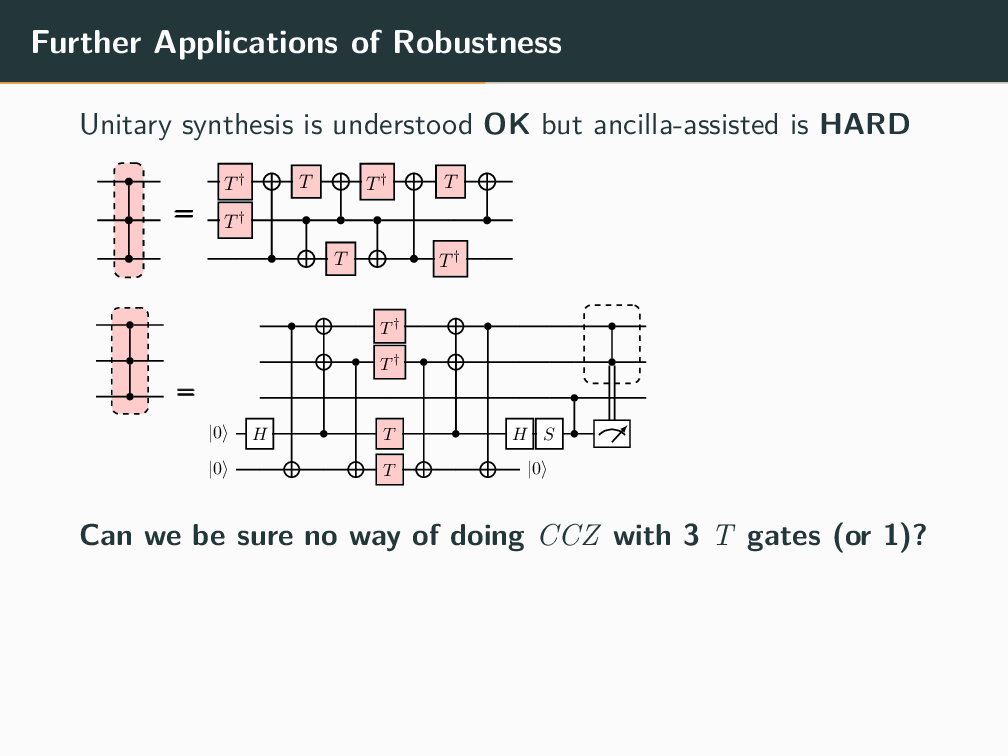
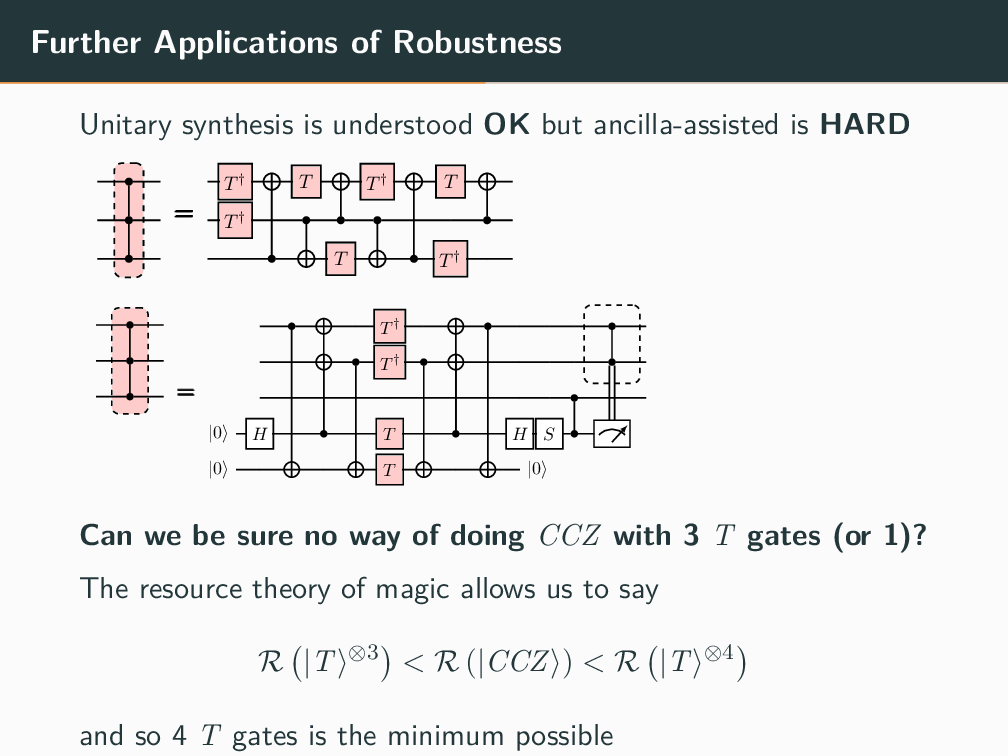
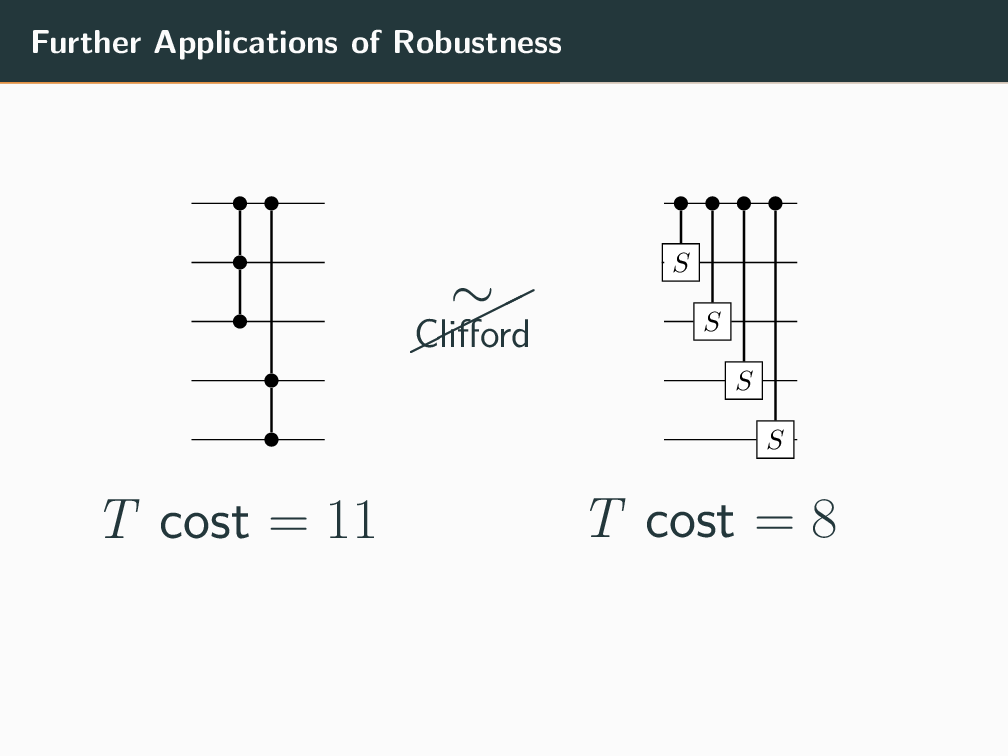
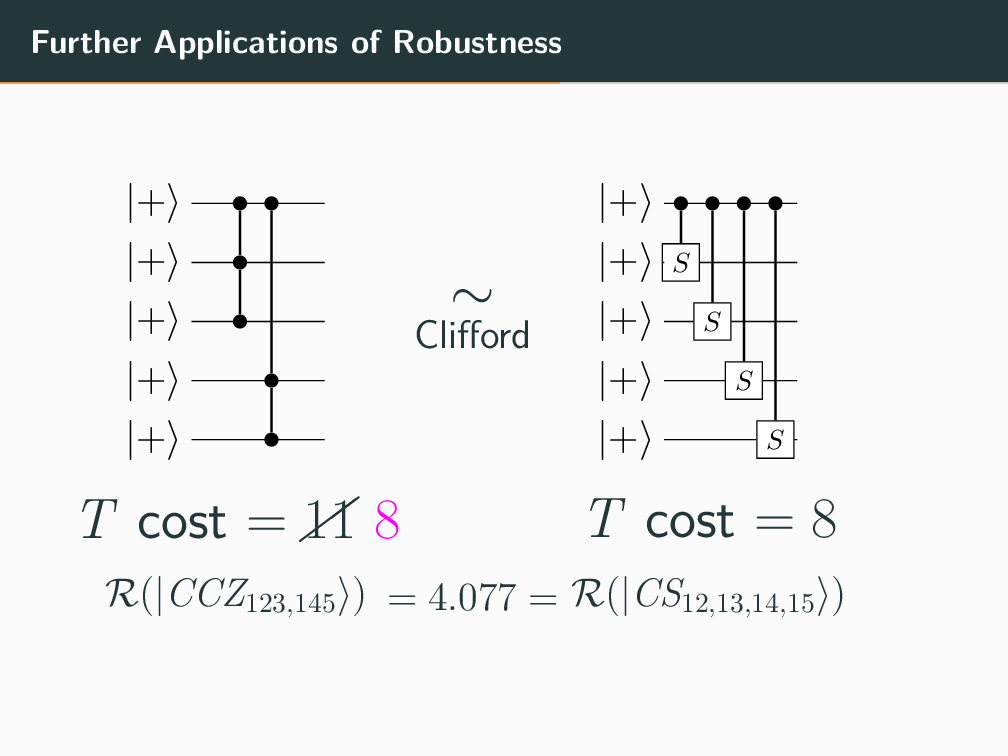
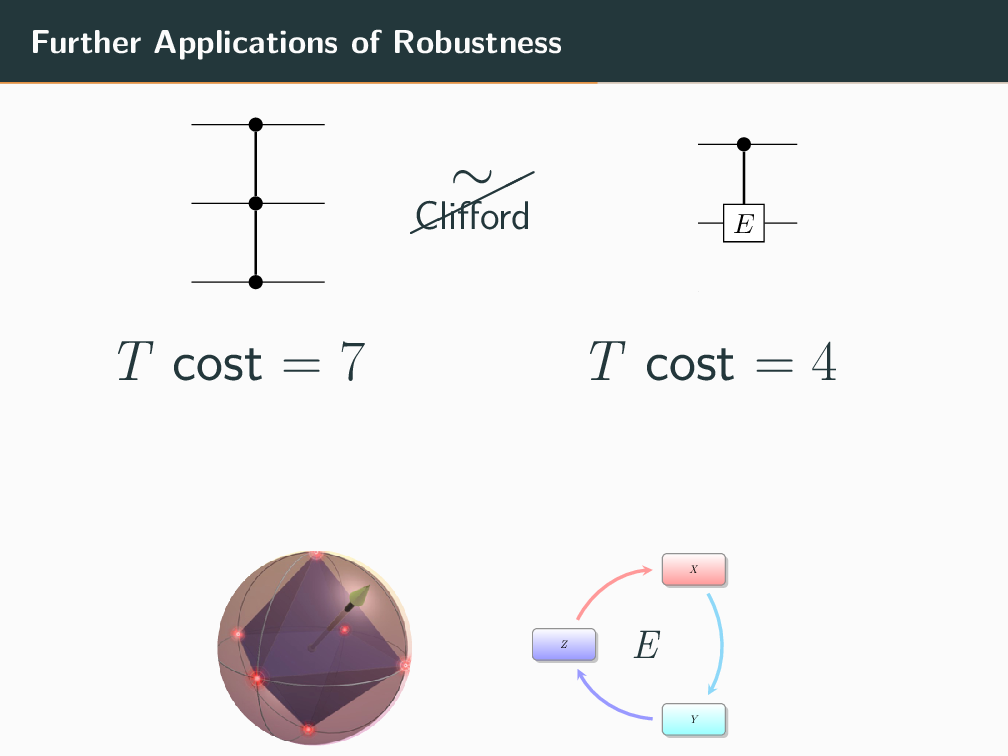
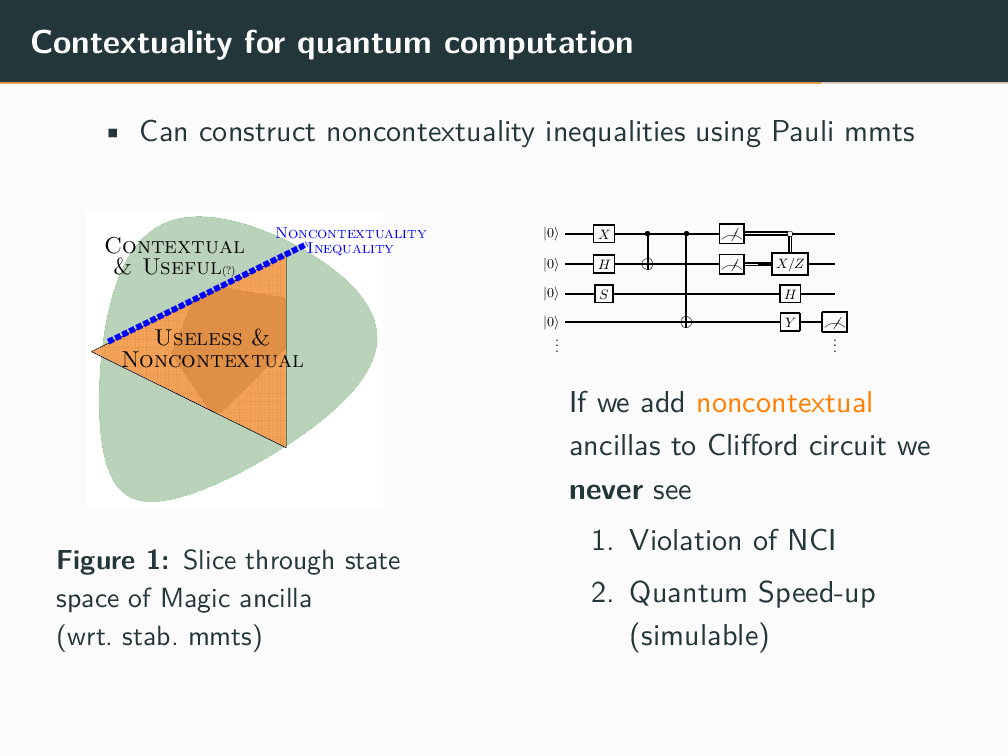
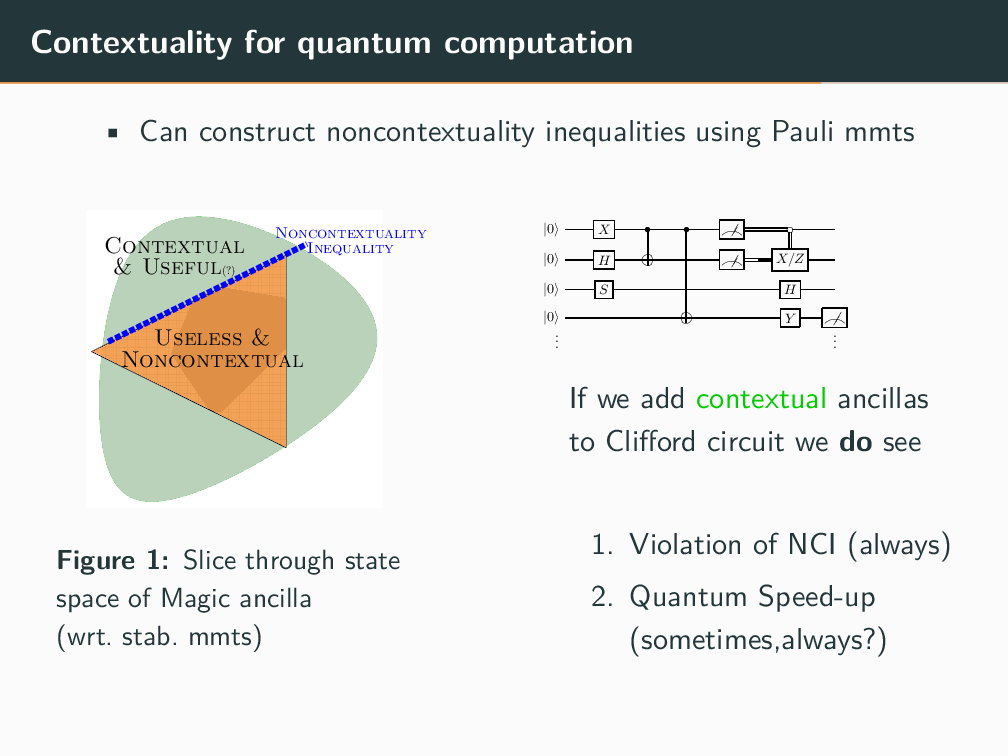
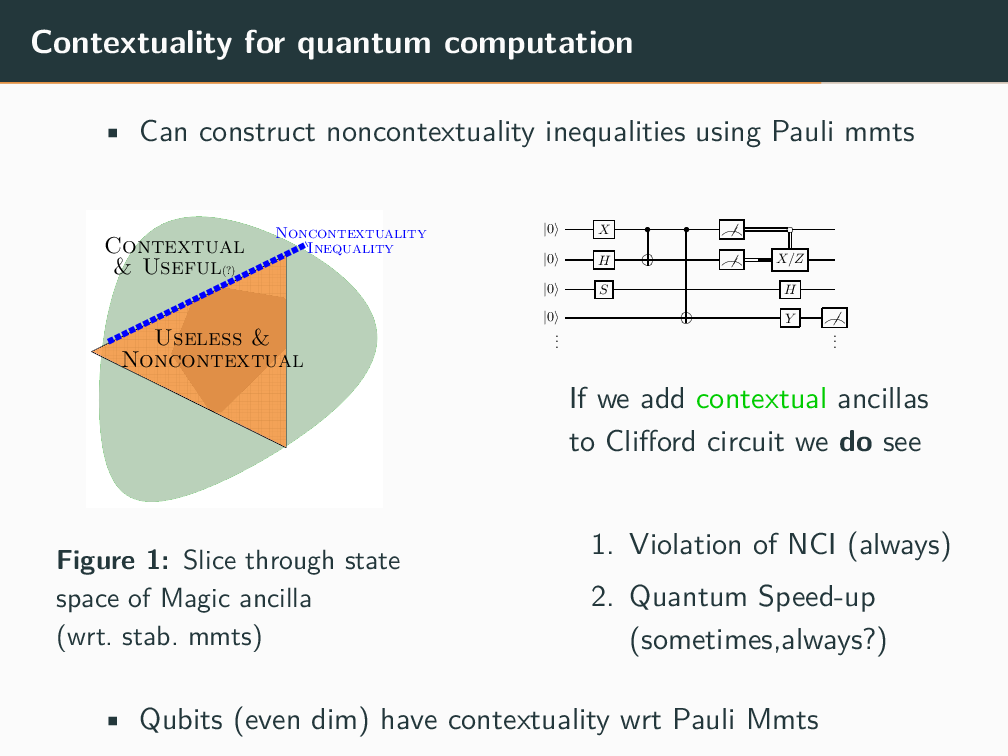
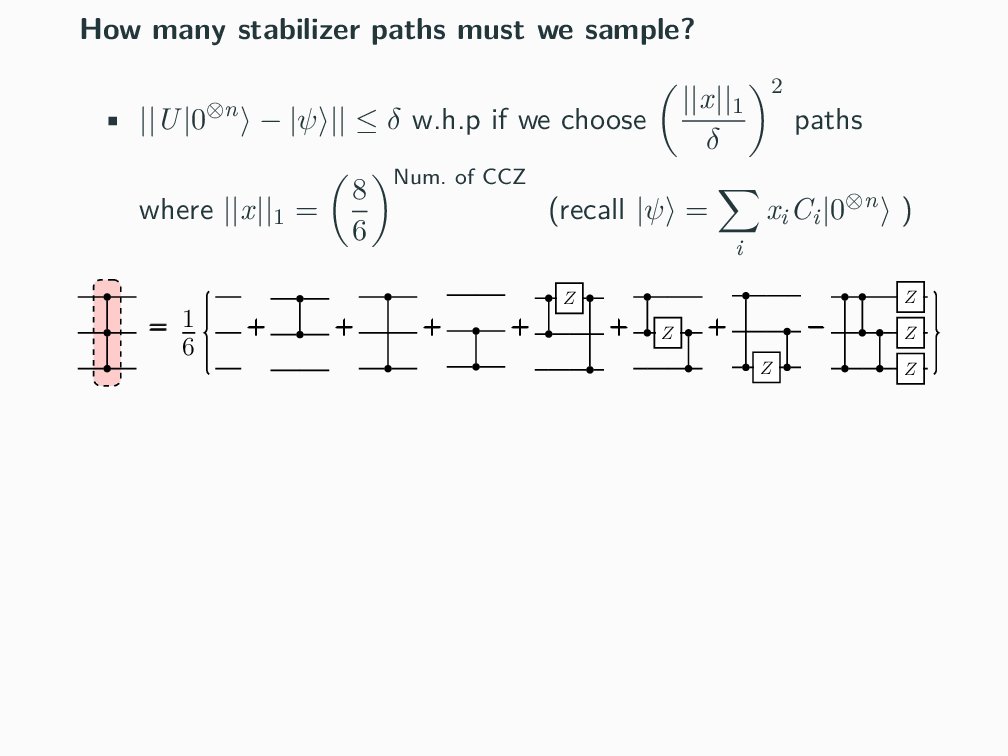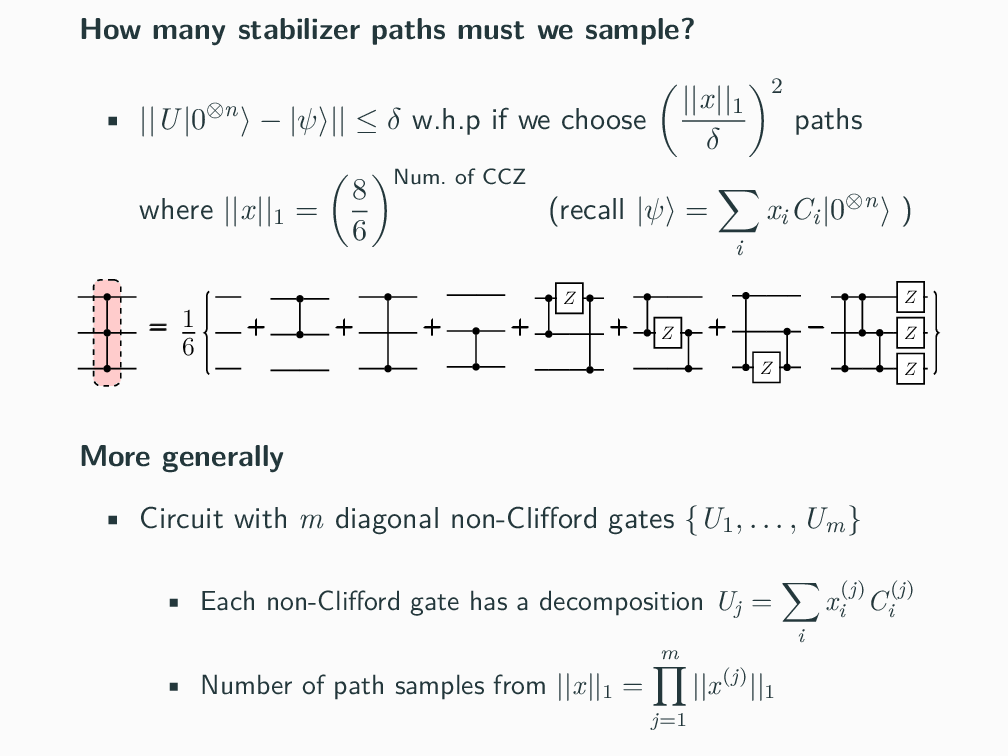Topics in Stabilizer Quantum Computation
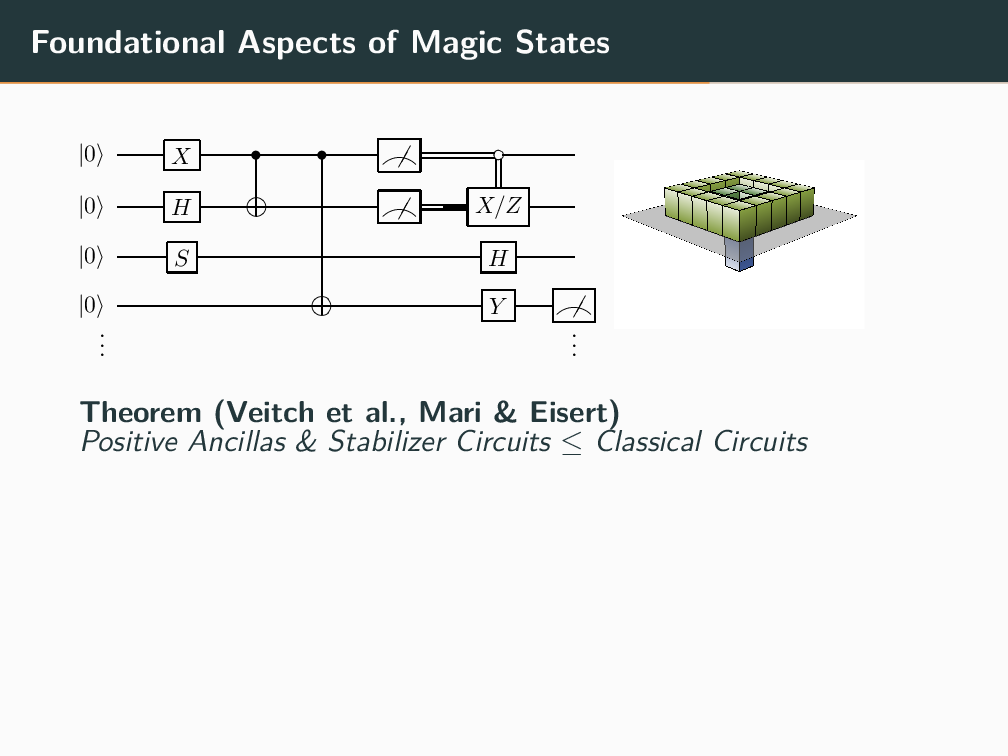
The central question in quantum information theory is to delineate the operational capabilities achievable under the rules of quantum mechanics but not achievable with classical physics. As such, it can be useful to tinker with hypothetical theories having different sets of allowed state preparations, transformations and measurements; different combinations can give us theories that are less powerful than, equal to, or more powerful than quantum mechanics. When we attempt to understand the computational power of circuits, so-called stabilizer circuits comprise a restricted class that are provably weaker than a general ("universal") quantum computer. For stabilizer circuits, the description of the achievable states and their updates is efficient leading to a classical simulation algorithm that is polynomial in the number of qubits. Remarkably, it is easy to boost the power of stabilizer circuits to that of a universal quantum computer by adding access to non-stabilizer states or operations. When error-correction is used these additional states or operations are typically very costly. All of the above naturally suggests a few questions that I will address:
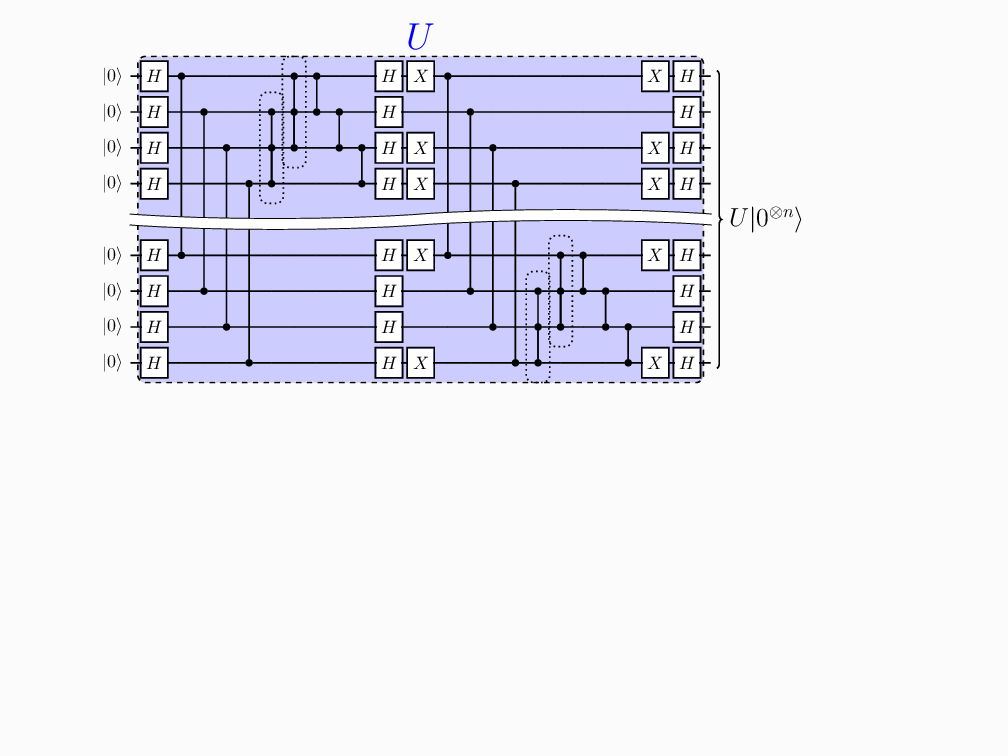
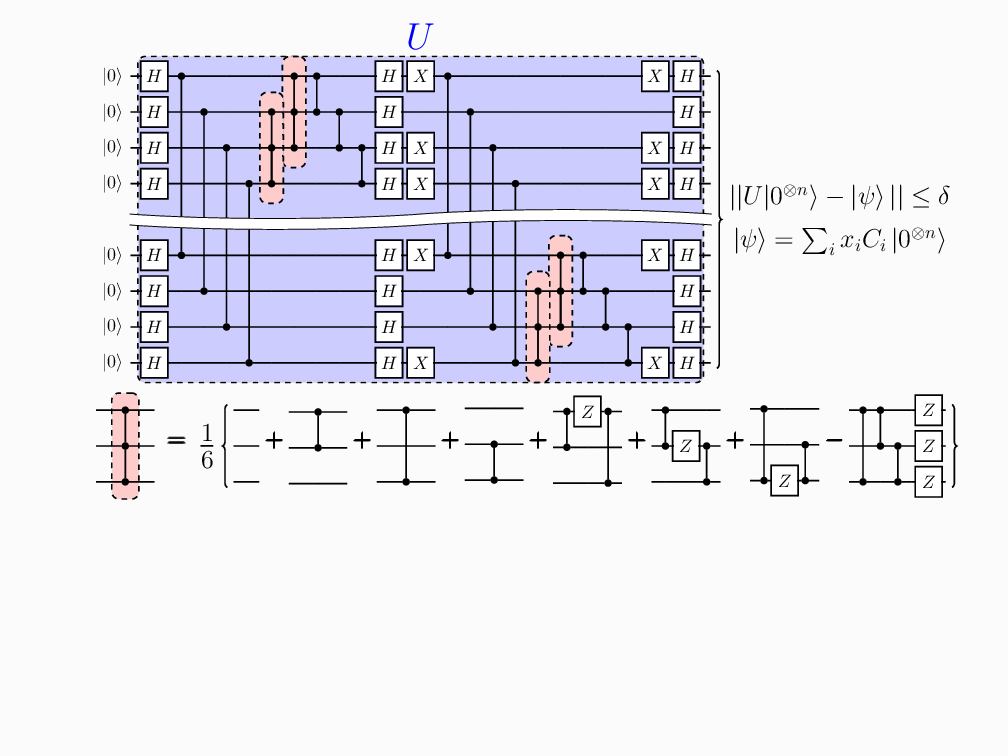
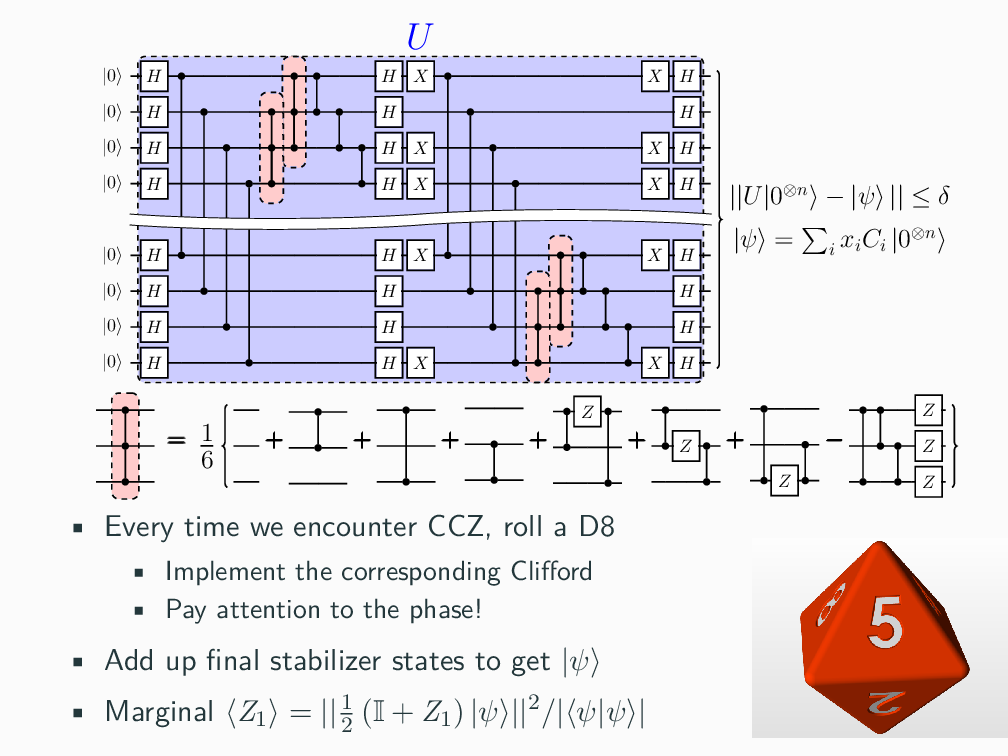
1) How should we classically simulate stabilizer circuits interspersed with a few non-stabilizer gates, and how does the runtime scale?
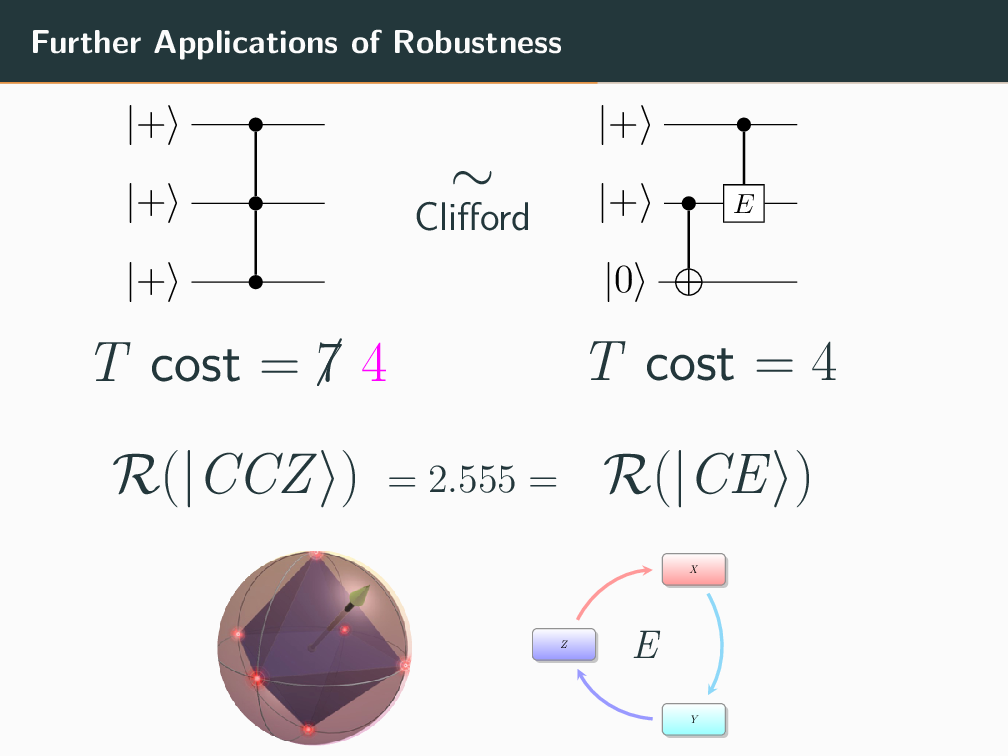
2) How can we minimize the use of costly non-stabilizer operations?
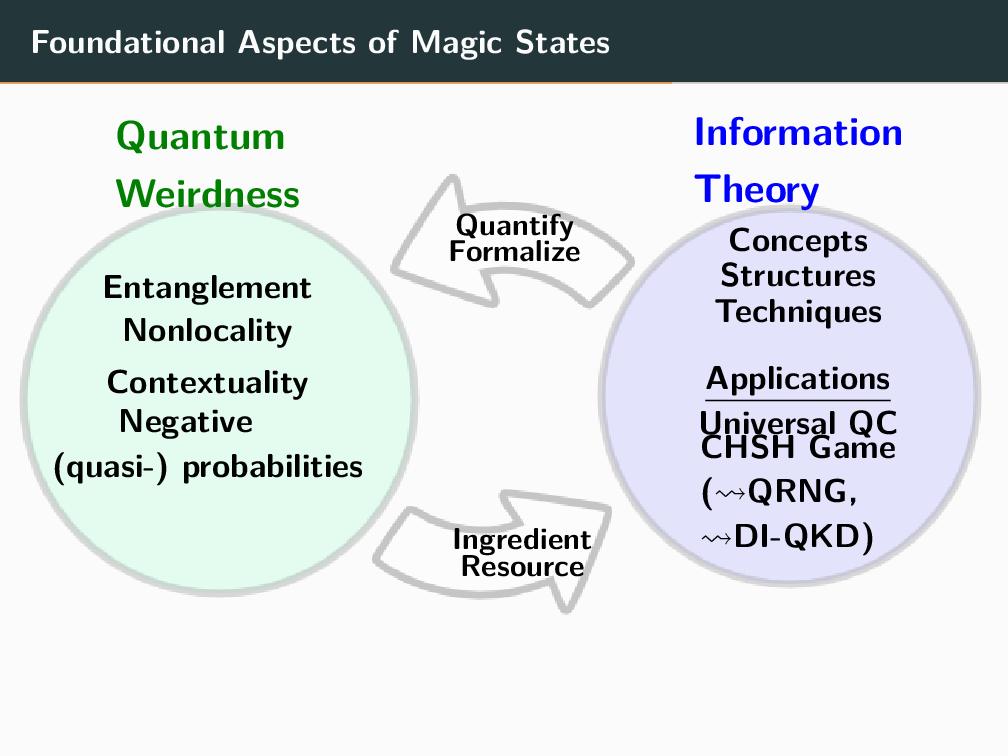
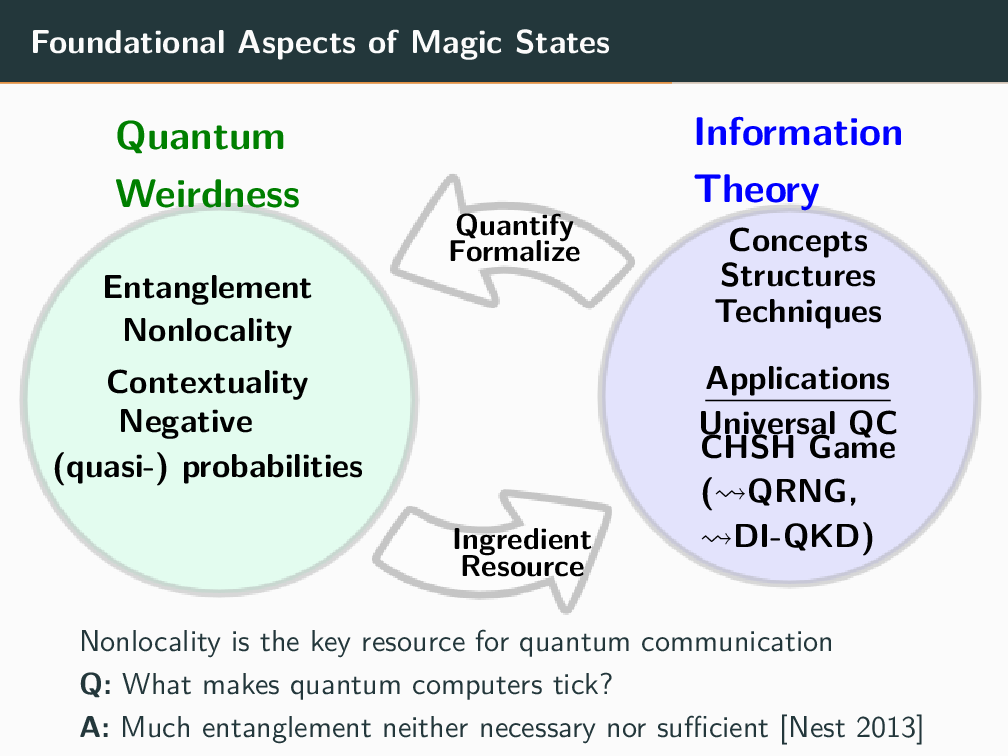
3) What quantum mechanical property is missing from stabilizer circuits but present in universal quantum computers?